Ctrl+K

推論

推論#

in English or the language of your choice. 

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import wooldridge

from statsmodels.formula.api import ols
from scipy.stats import t, f

# 警告メッセージを非表示
import warnings
warnings.filterwarnings("ignore")

説明：仮説検定#

仮説検定は以下の手順でおこなう。

  1. 母集団のパラメータについて帰無仮説（Null Hypothesis）と対立仮説（Alternative Hypothesis）を設定する。

    • 帰無仮説は棄却するかどうかの判断の対象となる仮説（例えば，\(\hat{\beta}_1=0\)）

    • 対立仮説は帰無仮説に相反する仮説（例えば，\(\hat{\beta}_1\neq 0\)）

  2. 適切な検定統計量を決め，判定するための有意水準を予め決める。

    • 有意水準 ＝ 下で説明する第一種過誤の確率

  3. 計算した検定統計量の値と有意水準に対応する値を比較することにより，帰無仮説を棄却するかしないかを判断する。２つの可能性しかない。

    • 帰無仮説を棄却する（対立仮説を採択する）。

    • 帰無仮説を棄却できない（対立仮説を採択できない）。

検定をおこなう際には間違いが発生する。それをまとめたのが次の表である。

帰無仮説は真

帰無仮説は偽

帰無仮説を棄却できない

正しい結論

第２種過誤

帰無仮説を棄却

第１種過誤

正しい結論

検定を警察の行動に例えて次のように考えることもできる。

  • 帰無仮説 \(\Rightarrow\) 「無罪」

  • 帰無仮説の棄却 \(\Rightarrow\) 「逮捕」

  • 帰無仮説を棄却しない \(\Rightarrow\) 「逮捕しない」

  • 第１種過誤 \(\Rightarrow\)「冤罪で逮捕」

  • 第２種過誤 \(\Rightarrow\)「真犯人を取り逃がす」

無実は真

無実は偽

逮捕しない

正しい結論

取り逃す

逮捕

冤罪

正しい結論

  • 統計的優位性とは，帰無仮説が正しい場合，帰無仮説の内容が発生した確率が非常に低い場合を指す。即ち，発生イベントが非常に起こりにくく，偶然の可能性が非常に高い場合である。

  • 第一種過誤は，帰無仮説が正しい場合に棄却すると発生する。慣例でその確率を\(\alpha\)で表す。\(\alpha=0.05\)がよく使われるが，これを使う場合，間違って正しい帰無仮説を棄却する確率は最大5%まで許容するという意味になる。

\(t\)検定#

説明：\(t\)値と\(p\)値#

新たな仮定を導入する。

  • 仮定６：誤差項は説明変数は独立であり正規分布に従う（誤差項の正規性）

\[u\sim N\left(0,\sigma^2\right)\]

仮定１〜６をClassical Linear Model (CLM) Assumptions（CLM仮定）と呼ぶ。

CLM仮定の下では：

  • OLS推定量は正規分布に従う。

    \[ \hat{\beta}_j\sim N\left(\beta_j,\text{Var}\left(\hat{\beta}_j\right)\right) \]

  • OLS推定量の標準誤差を使い標準化すると以下が成立する。

    \[ \frac{\hat{\beta}_j-\beta_j}{\text{se}\left(\hat{\beta}_j\right)}\sim t_{n-k-1} \]

    ここで\(t_{n-k-1}\)は自由度\(n-k-1\)の\(t\)分布を表している。\(n\)は標本の大きさ，\(k\)は定数項以外の説明変数の数である（定数項がある場合）。

この関係を使うことによりOLS推定量の検定が可能となる。

  • 帰無仮説：\(H_0:\hat{\beta}_j=0\)

    • \(H_0\)が正しい場合，\(t\)統計量は次の分布に従う。

      \[ t_{\hat{\beta}_j}\equiv\frac{\hat{\beta}_j}{\text{se}\left(\hat{\beta}_j\right)}\sim t_{n-k-1} \]

  • 対立仮説と棄却ルール（\(\alpha=\)有意水準）：

    • 右側検定：\(H_A:\hat{\beta}_j>0\)

      \[ t_{\hat{\beta}_j}>t_c(\alpha)>0\quad\Rightarrow\quad H_0\text{を棄却する} \]

    • 左側検定：\(H_A:\hat{\beta}_j<0\)

      \[ t_{\hat{\beta}_j}<t_c(\alpha)<0\quad\Rightarrow\quad H_0\text{を棄却する} \]

    • 両側検定：\(H_A:\hat{\beta}_j\neq 0\)

      \[ \left|t_{\hat{\beta}_j}\right|>t_c(\alpha/2)>0\quad\Rightarrow\quad H_0\text{を棄却する} \]

ここで，\(t_c(\alpha)\)は有意水準\(\alpha\)に対応する片側検定の棄却臨界値であり、\(t_c(\alpha/2)\)は有意水準\(\alpha\)に対応する両側検定の棄却臨界値である。

＜\(p\)値＞

\(p\)値は，帰無仮説が正しい場合に観測された事象が起こった確率である。即ち、\(p\)値が非常に低い場合（例えば、0.01）、帰無仮説のもとで発生した事象は非常に起こりにくく，偶然の可能性が非常に高いことを意味する。また、第一種過誤の確率は非常に低いことも意味する。

\(p\)値を使う場合の検定手順

  • 棄却するための有意水準 \(\alpha\)を決める（例えば，0.05）

  • \(p値\leq \alpha\)の場合，\(\text{H}_0\)を棄却

\(t\)値と\(p\)値の例#

定数項があり

  • 有意水準：\(\alpha=0.05\)

  • 標本の大きさ：\(n=30\)

  • 説明変数の数（定数項以外）：\(k=5\)

の場合を考えよう。

\(t\)値#

右側検定の場合の\(t_c(0.05)\)は次の値となる。

a = 0.05
dof = 30-5-1

t_right = t.ppf(1-a, dof)  # t.ppfについてはscipy.statsを参照
t_right

1.7108820799094278

左側検定の場合の\(t_c(0.05)\)は次の値となる。

t_left = t.ppf(a, dof)
t_left

-1.7108820799094282

両側検定の場合の\(t_c(0.05)\)は、\(1-a/2\)を使うと次のコードとなる。

t_both = t.ppf(1-a/2, dof)
t_both

2.063898561628021

\(a/2\)を使うと次のコードで同じ値を計算できる。

abs(t.ppf(a/2,dof))

2.063898561628021

abs()は絶対値を計算する関数である。

\(p\)値#

\(p\)値の計算の例として上のt_right、t_left、t_bothを使ってみる。

右側検定で\(t_{\hat{\beta}_j}=\) t_rightの場合，\(p\)値は次の値になる。

1-t.cdf(t_right, dof)   # t.cdfについてはscipy.statsを参照

0.050000000000000044

左側検定で\(t_{\hat{\beta}_j}=\) t_leftの場合，\(p\)値は次の値になる。

t.cdf(t_left, dof)

0.050000000000000024

両側検定で\(\left|t_{\hat{\beta}_j}\right|=\) t_bothの場合，\(p\)値は次の値になる。

2*( 1-t.cdf(t_both, dof) )

0.05000000000000049
_images/t_p_values.jpeg

Fig. 3 上で計算した数値の図示（累積分布関数と確率密度関数は\(t\)分布）。#

回帰分析と\(t\)検定#

gpa1のデータを使った回帰分析を考えよう。

gpa = wooldridge.data('gpa1')
wooldridge.data('gpa1',description=True)

name of dataset: gpa1
no of variables: 29
no of observations: 141

+----------+--------------------------------+
| variable | label                          |
+----------+--------------------------------+
| age      | in years                       |
| soph     | =1 if sophomore                |
| junior   | =1 if junior                   |
| senior   | =1 if senior                   |
| senior5  | =1 if fifth year senior        |
| male     | =1 if male                     |
| campus   | =1 if live on campus           |
| business | =1 if business major           |
| engineer | =1 if engineering major        |
| colGPA   | MSU GPA                        |
| hsGPA    | high school GPA                |
| ACT      | 'achievement' score            |
| job19    | =1 if job <= 19 hours          |
| job20    | =1 if job >= 20 hours          |
| drive    | =1 if drive to campus          |
| bike     | =1 if bicycle to campus        |
| walk     | =1 if walk to campus           |
| voluntr  | =1 if do volunteer work        |
| PC       | =1 of pers computer at sch     |
| greek    | =1 if fraternity or sorority   |
| car      | =1 if own car                  |
| siblings | =1 if have siblings            |
| bgfriend | =1 if boy- or girlfriend       |
| clubs    | =1 if belong to MSU club       |
| skipped  | avg lectures missed per week   |
| alcohol  | avg # days per week drink alc. |
| gradMI   | =1 if Michigan high school     |
| fathcoll | =1 if father college grad      |
| mothcoll | =1 if mother college grad      |
+----------+--------------------------------+

Christopher Lemmon, a former MSU undergraduate, collected these data
from a survey he took of MSU students in Fall 1994.

このデータセットを使い，次の問題を考える。ミシガン州立大学で学生のGPA（colGDP）は以下の変数とどのような関係にあるのか。

  • hsGPA：高校のGPA

  • ACT：米国大学進学適性試験

  • skipped：週平均の講義欠席回数

formula_gpa = 'colGPA ~ hsGPA + ACT + skipped'
res_gpa = ols(formula_gpa, data=gpa).fit()

res_gpaの属性tvaluesを使い\(t\)値を表示してみる。

res_gpa.tvalues

Intercept    4.191039
hsGPA        4.396260
ACT          1.393319
skipped     -3.196840
dtype: float64

この値を１つ１つ棄却臨界値と比べるのも手間がかかるので、次のような関数を作成し、任意の棄却臨界値に基づき両側検定を行うことも簡単にできる。

def significance_check(res, a=0.05):
    """
    定数項がある場合のt検定をおこなう。
    
    引数：
        res = statsmodelsによるOLS推定結果
        a = 有意水準（デフォルト：0.05）
    返り値：
        帰無仮説を棄却する場合はTrueを返す。
    """
    
    dof = res.nobs-res.df_model-1
    result = abs(res.tvalues) > t.ppf(1-a/2, dof)
    
    return pd.Series(result, index=res.tvalues.index)

＜コードの説明＞

"""と"""で囲まれた行は関数の説明であり、docstringと呼ばれる。docstringは覚え書きのようなもので、何ヶ月後の自分が読んだり、他の人が読む場合に便利となる。また、statsmodelsなどのパッケージは数多くの関数を使っており、それらにもdocstringが追加されているのが普通である。関数help()を使うとdocstringが表示される。

help(significance_check)

Help on function significance_check in module __main__:

significance_check(res, a=0.05)
    定数項がある場合のt検定をおこなう。
    
    引数：
        res = statsmodelsによるOLS推定結果
        a = 有意水準（デフォルト：0.05）
    返り値：
        帰無仮説を棄却する場合はTrueを返す。

次のコードでも同じ内容を確認できる。

significance_check?

関数を実行してみよう。

significance_check(res_gpa, 0.05)

Intercept     True
hsGPA         True
ACT          False
skipped       True
dtype: bool

res_gpaの属性pvaluesから\(p\)値を表示してみよう。

res_gpa.pvalues

Intercept    0.000050
hsGPA        0.000022
ACT          0.165780
skipped      0.001725
dtype: float64

print(res_gpa.summary().tables[1])

==============================================================================
                 coef    std err          t      P>|t|      [0.025      0.975]
------------------------------------------------------------------------------
Intercept      1.3896      0.332      4.191      0.000       0.734       2.045
hsGPA          0.4118      0.094      4.396      0.000       0.227       0.597
ACT            0.0147      0.011      1.393      0.166      -0.006       0.036
skipped       -0.0831      0.026     -3.197      0.002      -0.135      -0.032
==============================================================================

  • coef: OLS推定量（\(\hat{\beta}_j\)）

  • std err: OLS推定量の標準誤差（\(\text{se}(\hat{\beta}_j)\)）

  • t: \(t\)値

  • p: \(p\)値

  • [0.025 0.975]: 信頼区間（次の節を参照）

OLS推定量の標準誤差は属性.bseとして取得できる。

res_gpa.bse

Intercept    0.331554
hsGPA        0.093674
ACT          0.010565
skipped      0.025999
dtype: float64

信頼区間#

信頼区間の計算#

信頼区間は次のように定義される。

\[ \hat{\beta}_j\pm t_c(a)\cdot se\left(\hat{\beta}_j\right) \]

ここで，\(a\)は有意水準である。

\(a=0.05\)として信頼区間の解釈を考えよう。

（間違った解釈）
母集団の（真の）\(\beta_j\)の値が信頼区間に入る確率は95％である。

（正しい解釈）
標本を取りOLS推定値を計算するというプロセスを100回繰り返すとしよう。それぞれの標本は異なるため推定値\(\hat{\beta}_j\)と\(t\)値も異なることになり，100の異なる信頼区間が生成される。その内，母集団の（真の）\(\beta_j\)の値が信頼区間に入るのは概ね\((1-0.05)\times 100\)回=95回であり，概ね5回は入らない。更に，100回ではなく無限回繰り返すと，計算した信頼区間の95%には真の値が入り，5%には入らない。

紛らわしい解釈だが，次の理由でこの様な解釈となる。まずサイコロを考えよう。6が出る確率は1/6だが，これはサイコロの目がランダム変数だからである。当たり前だが，ランダム変数の場合に確率を考えることができる。このことを踏まえて，母集団の（真の）\(\beta_j\)の値を考えよう。サイコロの目と違って，\(\beta_j\)は定数として与えられており，ランダム変数ではない。従って，１つの信頼区間を計算した後に，その区間に（ランダム変数ではない）真の値が入るかについての確率を考えることは無意味なのである。更に言うと，\(\beta_j\)が信頼区間に入っているのか，もしくは，入っていないかの２つのケースしかなく，確率は1もしくは0にしかならないし，0と1の間の確率はあり得ないという事になる。一方，信頼区間の上限と下限の値はランダムであり，異なる標本を使い複数回にわたって信頼区間を計算すると，異なる上限値・下限値となる。この場合，ランダムな信頼区間が（観測不可能だが）定数である\(\beta_j\)を含むかの確率を考えることは意味があることであり，それが信頼区間の解釈となる。

ではgpaの例を考えよう。res_gpaのメソッドconf_int()を使い信頼区間を取得できる。

print(res_gpa.conf_int())

                  0         1
Intercept  0.733930  2.045178
hsGPA      0.226582  0.597050
ACT       -0.006171  0.035612
skipped   -0.134523 -0.031703

有意水準のオプションalpha=を指定することもできる（デフォルトは0.05）。有意水準が1％の場合は次のように指定する。

print(res_gpa.conf_int(alpha=0.01))

                  0         1
Intercept  0.523472  2.255635
hsGPA      0.167121  0.656511
ACT       -0.012877  0.042318
skipped   -0.151026 -0.015200

OLS推定値は1つの値を返す「点推定」だが，信頼区間は有意水準に基づく「区間推定」である。両方を確認することが大事である。例えば、ACTの信頼区間を考えよう。100回推定をした場合，母集団の\(\beta_{ACT}\)の値は95回この区間に入ることになるが，有意水準が1%でも5%でも0が含まれている。0の可能性が高いことを示している。

信頼区間の図示#

matplotlibのerrorbarを使い図示する。

coef = res_gpa.params      # 推定値
varname = coef.index       # 変数名
ci = res_gpa.conf_int()    # 信頼区間を　ci　に入れる
error = ci.iloc[:,1]-coef  # 信頼区間の幅の半分

plt.errorbar(x=coef[1:], y=varname[1:], xerr=error[1:], fmt='o',capsize=5)  # 切片以外のエラーバー
plt.axvline(0, color='red')  # 垂直線
pass
_images/6973e715fbfb70c80f4e8006db01b0e0cc6d7a0081bcda62d17583168f2abb93.png

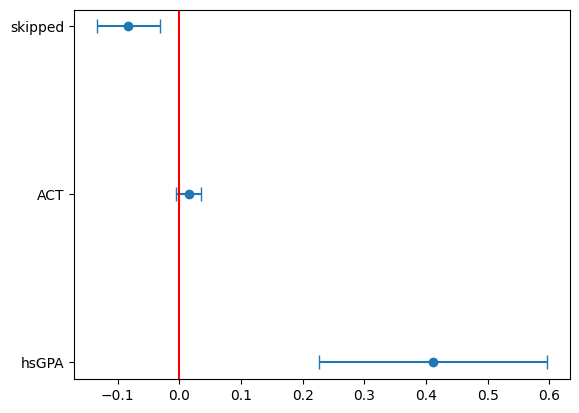
ACTの信頼区間に0が含まれることが分かる。

\(F\)検定#

説明#

回帰分析において複数のOLS推定量に何らかの制約が妥当かどうかを調べる際に使うのが\(F\)検定である。例えば，次の回帰式の場合

\[ y=\beta_0+\beta_1x_1+\beta_2x_2+\beta_3x_3+u \]

制約式の例として以下が挙げられる。

\(\beta_1=\beta_2=\beta_3=0\)

\(\beta_2=\beta_3=0\)

\(\beta_2=2\beta_3\)

帰無仮説と対立仮説は次のようになる。

  • 帰無仮説：\(\text{H}_0\)：制約が成立する

  • 対立仮説：\(\text{H}_A\)：制約は成立しない

検定手順

  1. 制約がない回帰式を推定する。

  2. 制約がある回帰式を推定する。

  3. 次の式に従い\(F\)値を計算する

    \[ F=\frac{\left(SSR_1-SSR_0\right)/q}{SSR_0/(n-k-1)} =\frac{\left(R_0^2-R_1^2\right)/q}{\left(1-R_0^2\right)/(n-k-1)} \sim F_{n-k-1}^q \]

    左辺の\(F\)は\(F\)値、右辺の\(F_{n-k-1}^q\)は自由度が\(q\)と\(n-k-1\)の\(F\)分布。

  4. 有意水準に基づく棄却臨界値と比べる（もしくは\(p\)値を有意水準と比べる）

上の式で

  • \(0\)：制約がない変数の添え字

  • \(1\)：制約がある変数の添え字

  • \(SSR\)：残差変動の平方和（Residual Sum of Squares）

  • \(R^2\)：決定係数

  • \(n\)：標本の大きさ

  • \(k\)：定数項以外の説明変数（制約がない回帰式）

  • \(q\)：制約式の数

名称：

  • \(q\)を「分子の自由度」と呼ぶ

  • \(n-k-1\)を「分母の自由度」と呼ぶ

＜棄却ルール＞

\(F>F_c(a)\)　\(\Rightarrow\)　\(\text{H}_0\)を棄却

  • \(F_c(a)\)：棄却臨界値

  • \(a\)：有意水準

（注意）\(F\)値は必ず正の値をとる。従って，\(t\)検定の「右片側検定」のパターンしか存在しない。

＜\(p\)値を使う場合の手順＞

  • 棄却するための有意水準 \(a\)を決める（例えば，0.05）

  • \(p値<a\)の場合，\(\text{H}_0\)を棄却

回帰分析#

例として米国野球選手（メジャーリーグ）に関するデータmlb1を使う。

mlb1 = wooldridge.data('mlb1')
wooldridge.data('mlb1',description=True)

name of dataset: mlb1
no of variables: 47
no of observations: 353

+----------+----------------------------+
| variable | label                      |
+----------+----------------------------+
| salary   | 1993 season salary         |
| teamsal  | team payroll               |
| nl       | =1 if national league      |
| years    | years in major leagues     |
| games    | career games played        |
| atbats   | career at bats             |
| runs     | career runs scored         |
| hits     | career hits                |
| doubles  | career doubles             |
| triples  | career triples             |
| hruns    | career home runs           |
| rbis     | career runs batted in      |
| bavg     | career batting average     |
| bb       | career walks               |
| so       | career strike outs         |
| sbases   | career stolen bases        |
| fldperc  | career fielding perc       |
| frstbase | = 1 if first base          |
| scndbase | =1 if second base          |
| shrtstop | =1 if shortstop            |
| thrdbase | =1 if third base           |
| outfield | =1 if outfield             |
| catcher  | =1 if catcher              |
| yrsallst | years as all-star          |
| hispan   | =1 if hispanic             |
| black    | =1 if black                |
| whitepop | white pop. in city         |
| blackpop | black pop. in city         |
| hisppop  | hispanic pop. in city      |
| pcinc    | city per capita income     |
| gamesyr  | games per year in league   |
| hrunsyr  | home runs per year         |
| atbatsyr | at bats per year           |
| allstar  | perc. of years an all-star |
| slugavg  | career slugging average    |
| rbisyr   | rbis per year              |
| sbasesyr | stolen bases per year      |
| runsyr   | runs scored per year       |
| percwhte | percent white in city      |
| percblck | percent black in city      |
| perchisp | percent hispanic in city   |
| blckpb   | black*percblck             |
| hispph   | hispan*perchisp            |
| whtepw   | white*percwhte             |
| blckph   | black*perchisp             |
| hisppb   | hispan*percblck            |
| lsalary  | log(salary)                |
+----------+----------------------------+

Collected by G. Mark Holmes, a former MSU undergraduate, for a term
project. The salary data were obtained from the New York Times, April
11, 1993. The baseball statistics are from The Baseball Encyclopedia,
9th edition, and the city population figures are from the Statistical
Abstract of the United States.

このデータセットを使い，年俸（salary）が次の変数とどう関係するかを考える。

  • years：メジャーリーグでプレイした期間（年）

  • gamesyr：年間出場回数

  • bavg：通算打率

  • hrunsyr：１シーズンあたりホームラン数

  • rbinsyr：１シーズンあたり打点

まず制約がない回帰分析をおこなう。

formula_0 = 'np.log(salary) ~ years + gamesyr + bavg + hrunsyr + rbisyr'
res_0 = ols(formula_0, data=mlb1).fit()

例１#

＜制約＞ bavg, hrunsyr, rbisyrはsalaryに影響を与えない。

\(H_0:\;\beta_{\text{bavg}}=\beta_{\text{hrunsyr}}=\beta_{\text{rbisyr}}=0\)

\(H_A:\;H_0は成立しない\)

制約がある場合の回帰分析

formula_1 = 'np.log(salary) ~ years + gamesyr'
res_1 = ols(formula_1, data=mlb1).fit()
手計算#

\(F\)値の計算

# 決定係数
r2_0 = res_0.rsquared
r2_1 = res_1.rsquared

n = res_0.nobs  # 標本の大きさ
k = res_0.df_model  # 定数項以外の説明変数の数
q = 3  # 制約式の数

# F値:
F = (r2_0 - r2_1) / (1 - r2_0) * (n - k - 1) / q
F

9.550253521951879

\(a=0.05\)の場合の棄却臨界値

a = 0.05
f.ppf(1-a, dfn=q, dfd=n-k-1)   # f.ppfについてはscipy.statsを参照

2.6306414891156504

従って\(H_0\)を棄却する。

\(p\)値

1-f.cdf(F, dfn=q, dfd=n-k-1)

4.473708139829391e-06
メソッドを使う#

制約式の定義

hypotheses = 'bavg = 0, hrunsyr = 0, rbisyr = 0'

res_0のメソッドf_testを使い、引数に上のセルで定義した制約式hypothesesを使う。

res_f_test = res_0.f_test(hypotheses)

res_f_testにF検定の結果を割り当てたが、そのメソッドsummary()を使い結果を表示する。

res_f_test.summary()

'<F test: F=9.550253521951985, p=4.473708139838421e-06, df_denom=347, df_num=3>'

上の結果にある記号の意味：

  • F：\(F\)値

  • p：\(p\)値

  • df_denom：分母の自由度

  • df_num：分子の自由度

手計算と同じ結果である。

例２#

＜制約＞ 定数項以外の全ての説明変数はsalaryに影響を与えない。

\(H_0:\;\beta_{\text{years}}=\beta_{\text{gamesyr}}=\beta_{\text{bavg}}=\beta_{\text{hrunsyr}}=\beta_{\text{rbisyr}}=0\)

\(H_A:\;H_0は成立しない\)

この場合，res_0のfvalueから\(F\)値，f_pvalueから\(p\)値を属性として取得できる。

res_0.fvalue

117.06032008521446

res_0.f_pvalue

2.938042293220727e-72

\(p\)値は非常に小さな値となっており、0.1%の有意水準でも帰無仮説を棄却できる。

例２の結果はOLS推定結果のメソッドsummary()で表示される表の中にあるF-statisticとProb(F-statistic)で確認することもできる。

print(res_0.summary())

                            OLS Regression Results                            
==============================================================================
Dep. Variable:         np.log(salary)   R-squared:                       0.628
Model:                            OLS   Adj. R-squared:                  0.622
Method:                 Least Squares   F-statistic:                     117.1
Date:                Fri, 26 Apr 2024   Prob (F-statistic):           2.94e-72
Time:                        01:22:49   Log-Likelihood:                -385.11
No. Observations:                 353   AIC:                             782.2
Df Residuals:                     347   BIC:                             805.4
Df Model:                           5                                         
Covariance Type:            nonrobust                                         
==============================================================================
                 coef    std err          t      P>|t|      [0.025      0.975]
------------------------------------------------------------------------------
Intercept     11.1924      0.289     38.752      0.000      10.624      11.760
years          0.0689      0.012      5.684      0.000       0.045       0.093
gamesyr        0.0126      0.003      4.742      0.000       0.007       0.018
bavg           0.0010      0.001      0.887      0.376      -0.001       0.003
hrunsyr        0.0144      0.016      0.899      0.369      -0.017       0.046
rbisyr         0.0108      0.007      1.500      0.134      -0.003       0.025
==============================================================================
Omnibus:                        6.816   Durbin-Watson:                   1.265
Prob(Omnibus):                  0.033   Jarque-Bera (JB):               10.197
Skew:                          -0.068   Prob(JB):                      0.00610
Kurtosis:                       3.821   Cond. No.                     2.09e+03
==============================================================================

Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
[2] The condition number is large, 2.09e+03. This might indicate that there are
strong multicollinearity or other numerical problems.
Contents