パネル・データ分析#
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import statsmodels.formula.api as smf
import wooldridge
from collections import OrderedDict
from linearmodels.panel.data import PanelData
from linearmodels.panel import PanelOLS, PooledOLS, RandomEffects, compare
from scipy.stats import gaussian_kde, norm, t
# 警告メッセージを非表示
import warnings
warnings.filterwarnings("ignore")
パネル・データを使った次のモデルについて説明する。
固定効果モデル(Fixed Effects Model)
ランダム効果モデル(Random Effects Model)
相関ランダム効果モデル(Correlated Random Effects Model)
固定効果モデル#
説明#
パネル・データを使う場合の問題は観察単位の異質性を捉える変数 \(a_i\) が説明変数 \(x_{it}\) と相関することにより,単純なOLS推定量に異質性バイアスが発生することである。その対処方法として,回帰式から\(a_i\)をなくす1階差分推定について説明した。この章では,同じように\(a_i\)をなくす代替推定法として固定効果推定(Fixed Effects Estimator)について考える。まず,その基礎となる固定効果モデル(Fixed Effects Model; FEモデル)について解説する。
次式を考えよう。
\(a_i\)は時間に依存せず,個体\(i\)特有の因子となっている。この\(i\)に固定された\(a_i\)が重要なモデルの要素なっているため固定効果モデルと呼ばれる。
\(i\)を所与として,両辺のそれぞれの変数の時間に対しての平均を計算すると次式となる。
(注意)\(a_i\)は時間に対して不変なため,\(a_i\)はそのままの値を取る。
(式1)と(式2)の差を取ると次の固定効果推定式が導出できる。
ここで
\(\ddot{y}_i=y_i-\bar{y}\)
\(\ddot{x}_i=x_i-\bar{x}\)
\(\ddot{u}_i=u_i-\bar{u}\)
は平均からの乖離(demeaned values)。
<仮定と推定量の性質>
(式1)のように回帰式は線形
標本のランダム抽出
\(x_{it}\)は時間と共に変動し、説明変数間の完全多重共線性は存在しない。
\(\text{E}(u_{it}|X_i,a_i)=0\)、即ち、\(a_i\) と \(x_{it}\), \(t=1,2,..,T\) を所与として \(u_{it}\) の平均は0
この仮定の下で,OLS推定量 \(\hat{\beta}_1\) は
不偏性を満たす。
\(T\)を一定として標本の大きさが十分に大きい場合,一致性を満たす。
固定効果推定量(Fixed Effects Estimator or FE Estimator)もしくは Within Estimatorと呼ばれる。
<良い点>
推定量は上述の仮定の下で不偏性・一致性が満たされる。
<悪い点>
時間に対して一定の説明変数は,\(a_i\)と同じように,(式3)に残らない。従って,時間不変の変数の効果を推定することはできない。
「手計算」による推定#
wagepanというデータセットを使い,賃金に対する労働組合などの変数の効果を推定する。
wagepan = wooldridge.data('wagepan')
wooldridge.data('wagepan', description=True)
name of dataset: wagepan
no of variables: 44
no of observations: 4360
+----------+------------------------+
| variable | label |
+----------+------------------------+
| nr | person identifier |
| year | 1980 to 1987 |
| agric | =1 if in agriculture |
| black | =1 if black |
| bus | |
| construc | =1 if in construction |
| ent | |
| exper | labor mkt experience |
| fin | |
| hisp | =1 if Hispanic |
| poorhlth | =1 if in poor health |
| hours | annual hours worked |
| manuf | =1 if in manufacturing |
| married | =1 if married |
| min | |
| nrthcen | =1 if north central |
| nrtheast | =1 if north east |
| occ1 | |
| occ2 | |
| occ3 | |
| occ4 | |
| occ5 | |
| occ6 | |
| occ7 | |
| occ8 | |
| occ9 | |
| per | |
| pro | |
| pub | |
| rur | |
| south | =1 if south |
| educ | years of schooling |
| tra | |
| trad | |
| union | =1 if in union |
| lwage | log(wage) |
| d81 | =1 if year == 1981 |
| d82 | |
| d83 | |
| d84 | |
| d85 | |
| d86 | |
| d87 | |
| expersq | exper^2 |
+----------+------------------------+
F. Vella and M. Verbeek (1998), “Whose Wages Do Unions Raise? A
Dynamic Model of Unionism and Wage Rate Determination for Young Men,”
Journal of Applied Econometrics 13, 163-183. I obtained the data from
the Journal of Applied Econometrics data archive at
http://qed.econ.queensu.ca/jae/. This is generally a nice resource for
undergraduates looking to replicate or extend a published study.
被説明変数
lwage:賃金(対数)
説明変数
union:労働組合参加(ダミー変数)married:未・既婚(ダミー変数)exper:労働市場参加年数d81:1981年のダミー変数d82:1982年のダミー変数d83:1983年のダミー変数d84:1984年のダミー変数d85:1985年のダミー変数d86:1986年のダミー変数d87:1987年のダミー変数
DataFrameのgroupbyを使って変数をグループ化する際に使う変数
nr:労働者のID
コメント
時間に対して変化しない変数は使えない。例えば,
educ(説明変数に入れば教育の収益率が推定可能である。)black,hisp(を使うと人種間の賃金格差も推定できる。)
は固定効果モデル回帰式には入れることができない。
# 説明変数のリスト
exog = ['married','union','expersq','d81','d82','d83','d84','d85','d86','d87']
# 全ての変数のリスト
var = ['lwage']+exog
# 使う変数だけで構成されるDataFrame
df = wagepan.loc[:,['nr']+var]
# varの平均からの乖離を計算(下の説明(1)を参照)
df_g = df.groupby('nr')
df_mean = df_g[var].transform('mean')
df_md = df.loc[:,var]-df_mean
# 説明変数の行列(下の説明(2)を参照)
X = df_md.loc[:,exog].values
# 被説明変数のベクトル
Y = df_md.loc[:,'lwage'].values
# OLSの計算
params = np.linalg.inv((X.T)@X)@(X.T)@Y
# 結果の表示(下の説明(3)を参照)
for idx, name in enumerate(exog):
print(f'{name}: {params[idx]:.4}')
married: 0.04668
union: 0.08
expersq: -0.005185
d81: 0.1512
d82: 0.253
d83: 0.3544
d84: 0.4901
d85: 0.6175
d86: 0.7655
d87: 0.925
説明(1)
df.groupby('nr'):nrでグループ化したオブジェクトを作成する(番外編のGapminderを参照)。df_g[var].transform('mean')df_g[var]:グループ化計算のためにvarの変数だけを使うことを指定する。.transform('mean'):指定された変数(var)のグループ内平均(それぞれのnr内での平均)を計算し,その平均で構成されるDataFrameを作成する。作成されたDataFrameの行数はdfと同じになり,グループ内平均が同じ列内でリピートされることになる。
df.loc[:,var]-df_mean:varのそれぞれの変数の平均からの乖離を計算する。df_mean = ...とdf_md = ...の2行を次のように1行にまとめることも可能。df_md = df_g[var].transform(lambda x: x-x.mean())
説明(2)
.valuesはDataFrameをnumpyのarrayとして返す。
説明(3)
enumerate(exog)はexogの変数のインデックスと変数名の両方をタプルとして返す。forループでenumerate()は,引数にリストやarrayを入れると2つの値を返す。1つ目の返り値:要素のインデックス
2つ目の返り値:要素自体
例えば,
enumerate(['A','B','C'])であれば,返り値は(0,'A'),(1,'B'),(2,'C')となる。
f'{name}: {params[idx]:.4}'f:以前説明したf-string{name}:exogの変数名を代入する。{params[idx]:.4}params[idx]:idx番目のparamsを代入する。:.4:小数点第4位までを表示する。
「手計算」の結果はlinearmodelsを使う結果と同じになることを下で確認する。
linearmodelsを使う計算#
EntityEffects#
linearmodelsにはPanelOLSモジュールがあり,その関数from_formula()を使うことにより,statsmodels同様,回帰式をy ~ xの文字列で書くことが可能となる。その際,次の点に注意すること。
固定効果推定をする場合,回帰式に
+ EntityEffectを含める。このオプションにより変数の平均からの乖離は自動で計算されることになる。
+ EntityEffectを含めないとPooledOLS(通常のOLS)と等しくなる。
まずwagepanをMultiIndex化する。これによりlinearmodelsを使いFD推定可能となる。
wagepan = wagepan.set_index(['nr','year'],drop=False)
wagepan.head()
| nr | year | agric | black | bus | construc | ent | exper | fin | hisp | ... | union | lwage | d81 | d82 | d83 | d84 | d85 | d86 | d87 | expersq | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| nr | year | |||||||||||||||||||||
| 13 | 1980 | 13 | 1980 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | ... | 0 | 1.197540 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 1981 | 13 | 1981 | 0 | 0 | 0 | 0 | 0 | 2 | 0 | 0 | ... | 1 | 1.853060 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 4 | |
| 1982 | 13 | 1982 | 0 | 0 | 1 | 0 | 0 | 3 | 0 | 0 | ... | 0 | 1.344462 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 9 | |
| 1983 | 13 | 1983 | 0 | 0 | 1 | 0 | 0 | 4 | 0 | 0 | ... | 0 | 1.433213 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 16 | |
| 1984 | 13 | 1984 | 0 | 0 | 0 | 0 | 0 | 5 | 0 | 0 | ... | 0 | 1.568125 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 25 |
5 rows × 44 columns
wagepan.info()
<class 'pandas.core.frame.DataFrame'>
MultiIndex: 4360 entries, (13, 1980) to (12548, 1987)
Data columns (total 44 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 nr 4360 non-null int64
1 year 4360 non-null int64
2 agric 4360 non-null int64
3 black 4360 non-null int64
4 bus 4360 non-null int64
5 construc 4360 non-null int64
6 ent 4360 non-null int64
7 exper 4360 non-null int64
8 fin 4360 non-null int64
9 hisp 4360 non-null int64
10 poorhlth 4360 non-null int64
11 hours 4360 non-null int64
12 manuf 4360 non-null int64
13 married 4360 non-null int64
14 min 4360 non-null int64
15 nrthcen 4360 non-null int64
16 nrtheast 4360 non-null int64
17 occ1 4360 non-null int64
18 occ2 4360 non-null int64
19 occ3 4360 non-null int64
20 occ4 4360 non-null int64
21 occ5 4360 non-null int64
22 occ6 4360 non-null int64
23 occ7 4360 non-null int64
24 occ8 4360 non-null int64
25 occ9 4360 non-null int64
26 per 4360 non-null int64
27 pro 4360 non-null int64
28 pub 4360 non-null int64
29 rur 4360 non-null int64
30 south 4360 non-null int64
31 educ 4360 non-null int64
32 tra 4360 non-null int64
33 trad 4360 non-null int64
34 union 4360 non-null int64
35 lwage 4360 non-null float64
36 d81 4360 non-null int64
37 d82 4360 non-null int64
38 d83 4360 non-null int64
39 d84 4360 non-null int64
40 d85 4360 non-null int64
41 d86 4360 non-null int64
42 d87 4360 non-null int64
43 expersq 4360 non-null int64
dtypes: float64(1), int64(43)
memory usage: 1.5 MB
次にPanelDataオブジェクトに変換しデータの特徴を調べる。
wagepanp = PanelData(wagepan)
wagepanp.shape
(44, 8, 545)
44: 変数の数
8: 期間数(年)
545:観察単位の数(人数)
次に,balanced もしくは unbalanced data set かを確認する。
(~wagepanp.isnull).all()
True
このデータ・セットはbalancedだが,unbalanced だったとしても,固定効果モデルの考え方や以下で説明するコードは変わらない。
実際に回帰式を書くことにする。使い方はstatsmodelsと似ている。
PanelOLSモジュールの関数.from_formulaを使い次のように引数を指定する。
EntityEffectsを加える。定数項を入れたい場合は,
1を回帰式に追加する。入れなければ定数項なしの推定となる。以下では時間ダミー
C(year)が入るので入れない。
formula_fe = 'lwage ~ married + union + expersq \
+d81+d82+d83+d84+d85+d86+d87 + EntityEffects'
固定効果モデルのインスタンスの作成
mod_fe = PanelOLS.from_formula(formula_fe, data=wagepan)
statsmodelsと同じように,そこから得た結果にメソッド.fit()を使い計算し結果が返される。
result_fe = mod_fe.fit()
<結果の表示方法>
res_feを実行。res_feに関数print()を使うと見やすい。res_feには属性summaryが用意されているが,表示方法1と同じ。summaryには属性tablesがあり,2つの表がリストとして格納されている。tables[0]:検定統計量の表(print()を使うと見やすくなる)tables[1]:係数の推定値やp値などの表(print()を使うと見やすくなる)
print(result_fe.summary.tables[1])
Parameter Estimates
==============================================================================
Parameter Std. Err. T-stat P-value Lower CI Upper CI
------------------------------------------------------------------------------
married 0.0467 0.0183 2.5494 0.0108 0.0108 0.0826
union 0.0800 0.0193 4.1430 0.0000 0.0421 0.1179
expersq -0.0052 0.0007 -7.3612 0.0000 -0.0066 -0.0038
d81 0.1512 0.0219 6.8883 0.0000 0.1082 0.1942
d82 0.2530 0.0244 10.360 0.0000 0.2051 0.3008
d83 0.3544 0.0292 12.121 0.0000 0.2971 0.4118
d84 0.4901 0.0362 13.529 0.0000 0.4191 0.5611
d85 0.6175 0.0452 13.648 0.0000 0.5288 0.7062
d86 0.7655 0.0561 13.638 0.0000 0.6555 0.8755
d87 0.9250 0.0688 13.450 0.0000 0.7902 1.0599
==============================================================================
(結果)
exper**2の係数が負で統計的有意性が高いのは,賃金に対して経験の効果は低減することを示している。marriedの係数は正であり,優位性が全くないわけではない。賃金の既婚プレミアムと呼ばれるものである。unionは労働組合の影響を示しているが,予測通りである。
\(R^2\)を表示してみる。
print(result_fe.summary.tables[0])
PanelOLS Estimation Summary
================================================================================
Dep. Variable: lwage R-squared: 0.1806
Estimator: PanelOLS R-squared (Between): 0.2386
No. Observations: 4360 R-squared (Within): 0.1806
Date: Sat, Sep 20 2025 R-squared (Overall): 0.2361
Time: 00:34:43 Log-likelihood -1324.8
Cov. Estimator: Unadjusted
F-statistic: 83.851
Entities: 545 P-value 0.0000
Avg Obs: 8.0000 Distribution: F(10,3805)
Min Obs: 8.0000
Max Obs: 8.0000 F-statistic (robust): 83.851
P-value 0.0000
Time periods: 8 Distribution: F(10,3805)
Avg Obs: 545.00
Min Obs: 545.00
Max Obs: 545.00
================================================================================
<この表にある\(R^2\)について>
\(R^2\)=\(R^2(\text{Within})\):(式3)を推定した際の\(R^2\)である(\(\ddot{y}_i\)が\(\ddot{x}_i\)によってどれだけ説明されたかを示す)。
\(R^2(\text{Between})\):(式2)を推定した際の\(R^2\)である(\(\hat{y}_i\)が\(\hat{x}_i\)によってどれだけ説明されたかを示す)。
\(R^2(\text{Overall})\):(式1)を推定した際の\(R^2\)である(\({y}_i\)が\({x}_i\)によってどれだけ説明されたかを示す)。
Hint
(式3)の回帰式には定数項はないため,上の計算で使った回帰式formula_feには定数項を表す1は省かれている。(式3)と整合性が取れたコードとなっており,直観的にも分かりやすい。では,formula_feに1を加えて次のように書き換えて計算するとどうなるのだろうか。
formula_fe = 'lwage ~ 1 + married + union + expersq \
+d81+d82+d83+d84+d85+d86+d87 + EntityEffects'
このコードを使うと定数項の推定値が計算されることになるが,(式3)とは整合性がないように見える。実際そうなのだが,linearmodelsでは,この場合の定数項の推定値は,(式3)の個体固有の因子である\(a_i\)の平均値を表す仕様になっている。formula_feに1+が追加されても,他の変数の推定値などは変わらない。確かめてみよう!
TimeEffects#
上の推定式では時間ダミー変数として使い,観察単位全てに共通な時間的な影響を捉えた。具体的には,インフレにより賃金は変化するが,その変化は全ての労働者には対して同じであり,その効果を時間ダミー変数が捉えている。それを時間効果と呼ぶ。このような時間ダミー変数を加えた理由は,時間効果が他の変数(例えば,married)の係数を「汚さない」ようにするためであり,よりピュアの効果を推定するためである。一方,linearmodelsでは,わざわざ時間ダミー変数を作らずともTimeEffectsを回帰式に追加することにより,時間効果を自動的に「排除」することができる。
formula_fe2 = 'lwage ~ married + union + expersq + TimeEffects + EntityEffects'
result_fe2 = PanelOLS.from_formula(formula_fe2, data=wagepan).fit()
print(result_fe2)
PanelOLS Estimation Summary
================================================================================
Dep. Variable: lwage R-squared: 0.0216
Estimator: PanelOLS R-squared (Between): -0.2717
No. Observations: 4360 R-squared (Within): -0.4809
Date: Sat, Sep 20 2025 R-squared (Overall): -0.2808
Time: 00:34:43 Log-likelihood -1324.8
Cov. Estimator: Unadjusted
F-statistic: 27.959
Entities: 545 P-value 0.0000
Avg Obs: 8.0000 Distribution: F(3,3805)
Min Obs: 8.0000
Max Obs: 8.0000 F-statistic (robust): 27.959
P-value 0.0000
Time periods: 8 Distribution: F(3,3805)
Avg Obs: 545.00
Min Obs: 545.00
Max Obs: 545.00
Parameter Estimates
==============================================================================
Parameter Std. Err. T-stat P-value Lower CI Upper CI
------------------------------------------------------------------------------
married 0.0467 0.0183 2.5494 0.0108 0.0108 0.0826
union 0.0800 0.0193 4.1430 0.0000 0.0421 0.1179
expersq -0.0052 0.0007 -7.3612 0.0000 -0.0066 -0.0038
==============================================================================
F-test for Poolability: 10.067
P-value: 0.0000
Distribution: F(551,3805)
Included effects: Entity, Time
result_feと同じ結果を確認できる。\(R^2\)の値は少し変わっているが,これは時間ダミーを入れて計算している訳ではないためである。
ダミー変数モデルとしての固定効果モデル#
固定効果推定量は,他の推定方法でも計算することができる。その1つがダミー変数推定である。アイデアは簡単で,観察単位のダミー変数を使い異質性を捉えるのである。推定方法も簡単で,(式1)に観察単位のダミー変数を加えて通常のOLS推定をおこなうだけである。
上で使ったwagepanを使い推定する。まず,観察単位のダミー変数として推定式にC(nr)を追加する
formula_dum = 'lwage ~ 1 + married + union + expersq \
+d81+d82+d83+d84+d85+d86+d87 + C(nr)'
PooledOLSモジュールの関数from_formulaを使って推定式を定義する。ここでPooledOLSとは,statsmodelsで使う通常のOLS推定と同じである。
result_dum = PooledOLS.from_formula(formula_dum, data=wagepan).fit()
nrのダミー変数が544あるため,そのまま結果を表示せずに,以下のセルにあるフィルターを使いメインの変数だけを表示する。下のコードのfilterで使う(result_dumに続く)属性・メソッドについて:
params:パラメーターを取得する属性index:paramsのインデックスを取得する属性str:indexにある文字列を操作可能なオブジェクトとして取得する属性contains():引数の文字列が文字列の中にある場合Trueを返すメソッド( ):括弧の中を先に評価するという意味tolist():リストに変換するメソッド
filter = (result_dum.params.index.str.contains('nr') == False).tolist()
result_dum.params[filter]
Intercept 0.933291
married 0.046680
union 0.080002
expersq -0.005185
d81 0.151191
d82 0.252971
d83 0.354444
d84 0.490115
d85 0.617482
d86 0.765497
d87 0.925025
Name: parameter, dtype: float64
3つの変数I(exper**2),married,unionの係数は固定効果モデルと等しいことが確認できる。
t値とp値の表示には次のコードを使う。
t値:
result_dum.tstats[filter]p値:
result_dum.pvalues[filter]
この場合,educ等の時間に対して不変の変数も推定式に加えることが可能である。一方,この方法はパラメーターの数は544+11=555あり,自由度が非常に低くなるのが欠点である。
(注意)
この推定式に時間に対して不変の変数(例えば,educ,blac,hisp,exper)を追加すると推定できない(エラーが発生する)。理由は,それらの変数はnrダミー変数と完全に同じ動きをするためである。
ランダム効果モデル#
説明#
ここでは,パネル・データを使い推定するランダム効果モデル(Random Effects Model; RE Model)を解説する。もう一度(式1)を考えよう。
(仮定) \(a_i\)は観察単位 \(i\) に対して一定であるが,\(i\)によってその値は異なる。
<固定効果モデルの仮定>
\(\text{Cov}\left(a_ix_{it}\right)\neq 0,\quad t=1,2,...,T\)
<ランダム効果モデルの仮定>
\(\text{Cov}\left(a_ix_{it}\right)=0,\quad t=1,2,...,T\)
この違いを念頭に(式1)を次式に書き換える。
ここで,
しかし,\(e_{it}\)と\(e_{its},\;t\ne s\)の共分散は
となる。即ち,誤差項が自己相関することになる。自己相関係数を計算してみよう。
\(\sigma_{a}^2=\text{Var}(a_i)\)(\(a_{i}\)の分散)
\(\sigma_{u}^2=\text{Var}(u_{it})\)(\(u_{it}\)の分散)
<含意>
\(a_i\)と\(x_{it}\)に相関がないため次の推定方法で一致性を満たす推定量を計算できる。
1つの時点でお横断面データを使いOLS推定(でも他のデータはどうする?)
全てのデータを使い何の区別もなくプールするPooled OLS推定(しかしパネル・データの特性を有効利用していない)。
時系列データを扱う場合,自己相関によりOLS推定量は効率性が低くなる。これは横断面データを扱う際の不均一分散が引き起こす問題と似ている。
1階差分推定や固定効果推定を使う必要はなく,使うと効率性が低い推定量となる。
1階差分推定や固定効果推定は\(\text{Cov}\left(a_ix_{it}\right)\neq 0,\quad t=1,2,...,T\)の場合に使う。
従って,問題は次の点:
より効率性が高い推定方法はどのようなものか。
その方法がランダム効果推定と言われるもので,固定効果のように,変数を平均からの部分的な乖離に変換することにより可能となる。具体的には,次式が推定式となる。
ここで
\(\overset{\circ}{y}_{it}=y_{it}-\theta\bar{y}_i\)
\(\overset{\circ}{x}_{it}=x_{it}-\theta\bar{x}_i\)
\(\overset{\circ}{e}_{it}=e_{it}-\theta\bar{e}_i\)
は変数の平均からの部分的な乖離であり,乖離の度合いを決める変数\(\theta\)は
と定義される。
(直観)
\(\sigma_a^2=0\)の場合\(\theta=0\)となり,\(a_i\)は\(i\)に対して一定であり観察単位の異質性はないということである。その場合は,通常のOLSで推定することがベストとなる。
\(\sigma_a^2\)が増加すると\(\theta\)は大きくなり,より大きな平均からの乖離が必要となる。極端な場合,\(\sigma_a^2\)が無限大に近づくと,\(\theta=1\)となり\(\overset{\circ}{y}=\ddot{y}\)となる。即ち,固定効果モデルはランダム効果モデルの極端な場合と解釈できる。
(注意)
\(\theta\)は事前にはわからないため推定する必要がある(
linearmodelsが自動的に計算する)。
<仮定と推定量の性質>
(式1)のように回帰式は線形
標本のランダム抽出
説明変数間の完全多重共線性は存在しない。
説明変数を所与として\(a_i\)の平均は一定(従って、\(\text{Cov}\left(a_ix_{it}\right)= 0\))。
この仮定の下で,RE推定量 \(\hat{\beta}_1\) は
一致性を満たす。しかし不偏性は満たさない。
(良い点)
時間に対して不変の説明変数があってもその係数を推定できる。
推定#
exper,educ,black,hispを加えて回帰式を定義する。
(注意)
時間ダミー変数の代わりにTimeEffectsを使わないように。
入れてもエラーは出ませんが,TimeEffectsは無視されて,時間ダミーがない結果と同じになります。
formula_re = 'lwage ~ 1 + married + union + expersq \
+ exper + educ + black + hisp \
+ d81 + d82 + d83 +d84 + d85 + d86 + d87'
RandomEffectsのモジュールにある関数from_formulaを使い計算する。
result_re = RandomEffects.from_formula(formula_re, data=wagepan).fit()
結果の表示。
print(result_re.summary.tables[1])
Parameter Estimates
==============================================================================
Parameter Std. Err. T-stat P-value Lower CI Upper CI
------------------------------------------------------------------------------
Intercept 0.0234 0.1514 0.1546 0.8771 -0.2735 0.3203
married 0.0638 0.0168 3.8035 0.0001 0.0309 0.0967
union 0.1059 0.0179 5.9289 0.0000 0.0709 0.1409
expersq -0.0047 0.0007 -6.8623 0.0000 -0.0061 -0.0034
exper 0.1058 0.0154 6.8706 0.0000 0.0756 0.1361
educ 0.0919 0.0107 8.5744 0.0000 0.0709 0.1129
black -0.1394 0.0480 -2.9054 0.0037 -0.2334 -0.0453
hisp 0.0217 0.0428 0.5078 0.6116 -0.0622 0.1057
d81 0.0404 0.0247 1.6362 0.1019 -0.0080 0.0889
d82 0.0309 0.0324 0.9519 0.3412 -0.0327 0.0944
d83 0.0202 0.0417 0.4840 0.6284 -0.0616 0.1020
d84 0.0430 0.0515 0.8350 0.4037 -0.0580 0.1440
d85 0.0577 0.0615 0.9383 0.3482 -0.0629 0.1782
d86 0.0918 0.0716 1.2834 0.1994 -0.0485 0.2321
d87 0.1348 0.0817 1.6504 0.0989 -0.0253 0.2950
==============================================================================
結果の解釈は下でする。
RE推定では\(\theta\)が重要な役目を果たすが,その値はresult_reの属性thetaを使うことによりDataFrameの形で表示できる。
balanced panel dataの場合,
thetaの値は一意で決まる。unbalanced panel dataの場合,
thetaは観察単位毎に計算される。
result_re.theta.iloc[0,:]
theta 0.645059
Name: 13, dtype: float64
上で説明したが\(\theta\)は\(u_a\)と\(u_it\)の分散である\(\sigma_a^2\)と\(\sigma_u^2\)に依存する。それらの値は,属性variance_decompositionを表示できる。以下の返り値の内容:
Effects:\(\sigma_a^2\)Residual:\(\sigma_u^2\)Percept due to Effects:\(\dfrac{\sigma_a^2}{\sigma_a^2+\sigma_u^2}\)
result_re.variance_decomposition
Effects 0.106946
Residual 0.123324
Percent due to Effects 0.464438
Name: Variance Decomposition, dtype: float64
相関ランダム効果モデル#
説明#
相関ランダム効果モデル(CREモデル)は,固定効果モデルとランダム効果モデルの中間的な位置にあり,両方を包含している。(式1)を考えよう。更に,観察不可能な固定効果\(a_i\)は説明変数と次の関係にあると仮定する。
\(\bar{x}_i=\dfrac{1}{T}\sum_{t=1}^Tx_{it}\)は説明変数の平均
\(\gamma\)は\(a_i\)と\(x_{it}\)の相関関係を捉える係数
\(r_i\)は説明変数\(x_{it}\)と相関しないと仮定,即ち,\(\text{Cov}\left(r_i\bar{x}_{it}\right)=0\)
(式5)を(式1)に代入すると次式を得る。
ここで
(含意)
\(\text{Cov}\left(r_i,\bar{x}_{it}\right)=0\;\Rightarrow\;\text{Cov}\left(v_i,\bar{x}_{it}\right)=0\)
REモデルと同じ構造となっており,違いは\(\bar{x}_i\)が追加されている。
linearmodelsのRandomEffectsモジュールが使える。
次の結果が成立する。
\[\hat{\beta}_{FE}=\hat{\beta}_{CRE}\]\(\hat{\beta}_{FE}\):固定効果推定量
\(\hat{\beta}_{CRE}\):相関ランダム効果推定量
この結果は,時間に対して不変な変数(例えば,
black)を含めても成立する
推定#
まず \(\bar{x}_i\) を計算し,それをwagepanに追加する。そのために次の関数を定義する。
(解説)
(1):関数の引数
dframe:データフレームori_col:平均を計算したい列new_col:計算した平均を入れる列
(2):
ori_colをグループ化し,グループ名とグループ平均からなる辞書の作成groupby(level=0):行の第1インデックスに従ってグループ化mean():グループ平均の計算to_dict():行の第1インデックスにあるグループ名をkey,グループ平均をvalueにする辞書の作成
(3):行の第1インデックスに該当するグループ平均が並ぶリストの作成
index.get_level_values(0):行の第1インデックスの値を取得to_series():seriesに変換map(dict):dictの内容に従って上のseriesの値をグループ平均に入れ替えるtolist():リストに変換
(4):
dframeにグループ平均が並ぶ新しい列が追加し,そのラベルをnew_colとする(5):
DataFrameを返す
def add_col_mean(dframe, ori_col, new_col): # (1)
dict = dframe.groupby(level=0)[ori_col].mean().to_dict() # (2)
mean = dframe.index.get_level_values(0).to_series().map(dict).tolist() # (3)
dframe.loc[:,new_col] = mean # (4)
return dframe # (5)
この関数を使い,married,union,expersqの平均を計算しwagepanに追加する。
(コメント)experは含めない。
wagepan = add_col_mean(wagepan, 'married', 'married_mean')
wagepan = add_col_mean(wagepan, 'union', 'union_mean')
wagepan = add_col_mean(wagepan, 'expersq', 'expersq_mean')
CRE推定と結果の表示
formula_cre = 'lwage ~ 1 + married + union + expersq \
+ married_mean + union_mean + expersq_mean \
+ d81 + d82 + d83 + d84 + d85 + d86 + d87'
result_cre = RandomEffects.from_formula(formula_cre, data=wagepan).fit()
print(result_cre)
RandomEffects Estimation Summary
================================================================================
Dep. Variable: lwage R-squared: 0.1711
Estimator: RandomEffects R-squared (Between): 0.0967
No. Observations: 4360 R-squared (Within): 0.1806
Date: Sat, Sep 20 2025 R-squared (Overall): 0.1355
Time: 00:34:45 Log-likelihood -1609.8
Cov. Estimator: Unadjusted
F-statistic: 69.027
Entities: 545 P-value 0.0000
Avg Obs: 8.0000 Distribution: F(13,4346)
Min Obs: 8.0000
Max Obs: 8.0000 F-statistic (robust): 69.027
P-value 0.0000
Time periods: 8 Distribution: F(13,4346)
Avg Obs: 545.00
Min Obs: 545.00
Max Obs: 545.00
Parameter Estimates
================================================================================
Parameter Std. Err. T-stat P-value Lower CI Upper CI
--------------------------------------------------------------------------------
Intercept 1.1537 0.0502 22.979 0.0000 1.0552 1.2521
married 0.0467 0.0183 2.5522 0.0107 0.0108 0.0825
union 0.0800 0.0193 4.1475 0.0000 0.0422 0.1178
expersq -0.0052 0.0007 -7.3693 0.0000 -0.0066 -0.0038
married_mean 0.1618 0.0469 3.4518 0.0006 0.0699 0.2536
union_mean 0.1612 0.0526 3.0653 0.0022 0.0581 0.2644
expersq_mean 0.0032 0.0009 3.4362 0.0006 0.0014 0.0050
d81 0.1512 0.0219 6.8959 0.0000 0.1082 0.1942
d82 0.2530 0.0244 10.371 0.0000 0.2052 0.3008
d83 0.3544 0.0292 12.134 0.0000 0.2972 0.4117
d84 0.4901 0.0362 13.544 0.0000 0.4192 0.5611
d85 0.6175 0.0452 13.663 0.0000 0.5289 0.7061
d86 0.7655 0.0561 13.654 0.0000 0.6556 0.8754
d87 0.9250 0.0687 13.465 0.0000 0.7903 1.0597
================================================================================
2つの利点#
CREモデルの2つの利点を解説する。
FE対RE検定#
FEモデルとREモデルのどちらが適しているかを調べることができるHausman検定というものがある。CREモデルを使うことにより,同様の検定が簡単に行える。(式6)を考えよう。
\(\gamma=0\)の場合,REモデルの(式5)と同じになり,REモデルが妥当ということになる。
\(\gamma\neq 0\)の場合,\(a_i\)と\(\bar{x}_{i}\)は相関することになり,これは\(\text{Cov}\left(a_i,{x}_{it}\right)\neq 0\)を意味し,FEモデルが妥当な推定方法となる。
この考えを利用して,次の帰無仮説と対立仮説のもとで\(\gamma\)の優位性を調べる。
\(\text{H}_0:\;\text{Cov}\left(a_i,x_{it}\right)=0\)
\(\text{H}_a:\;\text{Cov}\left(a_i,x_{it}\right)\neq 0\)
(コメント)
\(\gamma=0\)を棄却できれば上の\(\text{H}_0\)を棄却できる。
平均の変数が\(k\)ある場合は,\(\gamma_1=\gamma_2=\cdots=\gamma_k=0\)を検定する。
result_creのメソッドwald_test()を使う。引数には文字列で指定する。
# 検定する係数の値を設定する
restriction = 'married_mean = union_mean = expersq_mean = 0'
# 検定結果を表示する
result_cre.wald_test(formula=restriction)
Linear Equality Hypothesis Test
H0: Linear equality constraint is valid
Statistic: 35.6454
P-value: 0.0000
Distributed: chi2(3)
WaldTestStatistic, id: 0x136fd4170
p値が非常に小さいので,帰無仮説は棄却できる。従って,FEモデルが妥当だと結論づけることができる。
一定な変数を含める#
(式6)に時間に対して一定は変数(\(z_{i}\))を含めて
をRE推定しても次の結果は成立する。
この結果を利用して,以下では次の変数を加えて回帰式を設定する。
時間に対して一定な変数
educ,black,hisp
一定ではないが,FEにいれると推定できなかった変数
exper
formula_cre2 = 'lwage ~ 1 + married + union + expersq \
+ exper + educ + black + hisp \
+ married_mean + union_mean + expersq_mean \
+ d81 + d82 + d83 + d84 + d85 + d86 + d87'
result_cre2 = RandomEffects.from_formula(formula_cre2, data=wagepan).fit()
print(result_cre2.summary.tables[1])
Parameter Estimates
================================================================================
Parameter Std. Err. T-stat P-value Lower CI Upper CI
--------------------------------------------------------------------------------
Intercept -0.1288 0.1583 -0.8140 0.4157 -0.4391 0.1814
married 0.0467 0.0183 2.5520 0.0107 0.0108 0.0825
union 0.0800 0.0193 4.1473 0.0000 0.0422 0.1178
expersq -0.0052 0.0007 -7.3689 0.0000 -0.0066 -0.0038
exper -0.0504 0.0507 -0.9947 0.3200 -0.1499 0.0490
educ 0.0946 0.0110 8.6115 0.0000 0.0731 0.1161
black -0.1388 0.0492 -2.8193 0.0048 -0.2353 -0.0423
hisp 0.0048 0.0430 0.1110 0.9116 -0.0795 0.0891
married_mean 0.0970 0.0454 2.1382 0.0326 0.0081 0.1859
union_mean 0.1907 0.0507 3.7591 0.0002 0.0912 0.2901
expersq_mean 0.0103 0.0033 3.1135 0.0019 0.0038 0.0168
d81 0.2016 0.0552 3.6497 0.0003 0.0933 0.3099
d82 0.3538 0.1043 3.3923 0.0007 0.1493 0.5583
d83 0.5058 0.1549 3.2650 0.0011 0.2021 0.8094
d84 0.6919 0.2060 3.3580 0.0008 0.2879 1.0958
d85 0.8697 0.2575 3.3768 0.0007 0.3648 1.3746
d86 1.0681 0.3094 3.4525 0.0006 0.4616 1.6746
d87 1.2781 0.3615 3.5351 0.0004 0.5693 1.9869
================================================================================
もう一度,FE対RE検定を行ってみよう。検定統計量(Statistics)は減少したが,以前として帰無仮説は高い優位水準で棄却できる。
result_cre2.wald_test(formula=restriction)
Linear Equality Hypothesis Test
H0: Linear equality constraint is valid
Statistic: 26.0233
P-value: 0.0000
Distributed: chi2(3)
WaldTestStatistic, id: 0x136fd58e0
モデルの比較#
パネル・データを扱う場合の通常のアプローチは,使える推定法を使いその結果を比べることから始める。以下では以下のモデルを比べる。
通常のOLS
固定効果モデル
ランダム効果モデル
相関ランダムモデル
OLS#
linearmodelsのモジュールPooledOLSでは,観察単位や時間の区別なく全てのデータをプールしてOLS推定する。これは通常のOLSと同じ推定法と等しい。PooledOLSの関数from_formulaを使い,以下のように推定する。
formula_pool = 'lwage ~ 1 + married + union + expersq \
+ exper + educ + black + hisp \
+d81+d82+d83+d84+d85+d86+d87'
result_pool = PooledOLS.from_formula(formula_pool, data=wagepan).fit()
print(result_pool.summary.tables[1])
Parameter Estimates
==============================================================================
Parameter Std. Err. T-stat P-value Lower CI Upper CI
------------------------------------------------------------------------------
Intercept 0.0921 0.0783 1.1761 0.2396 -0.0614 0.2455
married 0.1083 0.0157 6.8997 0.0000 0.0775 0.1390
union 0.1825 0.0172 10.635 0.0000 0.1488 0.2161
expersq -0.0024 0.0008 -2.9413 0.0033 -0.0040 -0.0008
exper 0.0672 0.0137 4.9095 0.0000 0.0404 0.0941
educ 0.0913 0.0052 17.442 0.0000 0.0811 0.1016
black -0.1392 0.0236 -5.9049 0.0000 -0.1855 -0.0930
hisp 0.0160 0.0208 0.7703 0.4412 -0.0248 0.0568
d81 0.0583 0.0304 1.9214 0.0548 -0.0012 0.1178
d82 0.0628 0.0332 1.8900 0.0588 -0.0023 0.1279
d83 0.0620 0.0367 1.6915 0.0908 -0.0099 0.1339
d84 0.0905 0.0401 2.2566 0.0241 0.0119 0.1691
d85 0.1092 0.0434 2.5200 0.0118 0.0243 0.1942
d86 0.1420 0.0464 3.0580 0.0022 0.0509 0.2330
d87 0.1738 0.0494 3.5165 0.0004 0.0769 0.2707
==============================================================================
比較表の作成#
今までの推定結果を表にまとめるために,linearmodelsの関数compareを使う。
表作成の順番:
keyが表示したい推定方法の名前,valueがその上で得た推定結果となる辞書を作るその辞書を
compareの引数としてつかう。
res = {'Pooled OLS':result_pool,
'FE': result_fe,
'RE': result_re,
'CRE': result_cre2
}
# compare(res)
このままでも良いか,この方法では推定結果を表示する順番を指定できない。例えば,OLS,FE,RE,CREの順番で左から並べたいとしよう。その場合,collectionsパッケージにある関数OrderedDictをつかう。{}の中で並べた順番をそのまま維持してくれる関数である。
res_ordered = OrderedDict(res)
print(compare(res_ordered))
Model Comparison
=========================================================================================
Pooled OLS FE RE CRE
-----------------------------------------------------------------------------------------
Dep. Variable lwage lwage lwage lwage
Estimator PooledOLS PanelOLS RandomEffects RandomEffects
No. Observations 4360 4360 4360 4360
Cov. Est. Unadjusted Unadjusted Unadjusted Unadjusted
R-squared 0.1893 0.1806 0.1806 0.1855
R-Squared (Within) 0.1692 0.1806 0.1799 0.1806
R-Squared (Between) 0.2066 0.2386 0.1853 0.2192
R-Squared (Overall) 0.1893 0.2361 0.1828 0.2013
F-statistic 72.459 83.851 68.409 58.165
P-value (F-stat) 0.0000 0.0000 0.0000 0.0000
===================== ============ ============ =============== ===============
Intercept 0.0921 0.0234 -0.1288
(1.1761) (0.1546) (-0.8140)
married 0.1083 0.0467 0.0638 0.0467
(6.8997) (2.5494) (3.8035) (2.5520)
union 0.1825 0.0800 0.1059 0.0800
(10.635) (4.1430) (5.9289) (4.1473)
expersq -0.0024 -0.0052 -0.0047 -0.0052
(-2.9413) (-7.3612) (-6.8623) (-7.3689)
exper 0.0672 0.1058 -0.0504
(4.9095) (6.8706) (-0.9947)
educ 0.0913 0.0919 0.0946
(17.442) (8.5744) (8.6115)
black -0.1392 -0.1394 -0.1388
(-5.9049) (-2.9054) (-2.8193)
hisp 0.0160 0.0217 0.0048
(0.7703) (0.5078) (0.1110)
d81 0.0583 0.1512 0.0404 0.2016
(1.9214) (6.8883) (1.6362) (3.6497)
d82 0.0628 0.2530 0.0309 0.3538
(1.8900) (10.360) (0.9519) (3.3923)
d83 0.0620 0.3544 0.0202 0.5058
(1.6915) (12.121) (0.4840) (3.2650)
d84 0.0905 0.4901 0.0430 0.6919
(2.2566) (13.529) (0.8350) (3.3580)
d85 0.1092 0.6175 0.0577 0.8697
(2.5200) (13.648) (0.9383) (3.3768)
d86 0.1420 0.7655 0.0918 1.0681
(3.0580) (13.638) (1.2834) (3.4525)
d87 0.1738 0.9250 0.1348 1.2781
(3.5165) (13.450) (1.6504) (3.5351)
married_mean 0.0970
(2.1382)
union_mean 0.1907
(3.7591)
expersq_mean 0.0103
(3.1135)
======================= ============== ============== ================= =================
Effects Entity
-----------------------------------------------------------------------------------------
T-stats reported in parentheses
marriedOLSでの結婚プレミアムは10%以上あるが,FEでは半減している。これは観察単位の異質性\(a_i\)に生産性が含まれており,「生産性が高い人(高い\(a_i\))は,結婚している可能性が高い」という考えと一貫性がある。即ち,\(\text{Cov}\left(a_i,x_{it}\right)>0\)となり,これによりOLSでは以下のようなバイアスが発生すると解釈できる。
既婚 \(\Rightarrow\) 生産性(\(a_i\))が高い \(\Rightarrow\) 賃金が上振れしやすい
未婚 \(\Rightarrow\) 生産性(\(a_i\))が低い \(\Rightarrow\) 賃金が下振れしやすい
FE推定法が示しているのは,そのようなバイアスを取り除いても,結婚プレミアムは存在する。考えられる理由は:
結婚は生産性を上昇させる
結婚は安定した生活を意味し,それに対して企業はより高い賃金を払う
REは推定値はFEに比較的に近い。これは\(\hat{\theta}>0.5\)の値にも現れている。
unionFEの値は労働組合の賃金に対する影響力を示している。
OLSとFEの推定値を比較すると,約0.1減少している。OLSは労働組合の影響力を過大評価しており,観察単位の異質性が大きく働いていることがわかる。
educ,black,hispOLSもREも推定値は似ている。
FD vs. FE#
1階差分モデルと固定効果モデルを比較する。
\(T=2\)の場合,FDとFEは同じ(if there is intercept in FE)
\(T\geq 3\)の場合:
GM仮定に対応する仮定の下ではFDもFEも不偏性・一致性を満たす。
誤差項に系列相関がない場合,FEの方が効率性が高い
誤差項の系列相関がある場合,FDの方が良い。
例えば,誤差項がランダム・ウォークの場合\(\Delta u_{it}\)は系列相関はない。
FD推定をして\(\Delta u_{it}\)を検定する。
\(N\)が少なく\(T\)が大きい場合(例:\(N=20\)と\(T=30\)),時系列の特性が強くなるので,FDの方が良い
実証研究では,FDとFEの結果の両方を報告すること。
FE vs. RE#
固定効果モデルとランダム効果モデルを比較する。
\(a_i\)はランダムか?
経済学の場合,説明変数は何らかの選択の結果の場合が多い。さらに,その選択が観察単位の特徴に依存する場合,\(\text{Cov}\left(a_ix_{it}\right)\neq 0\)となり,FEモデルの方が適切となる。
都道府県データのような場合,「大きな」母集団からランダムに抽出された説明変数とはならないかも知れない。むしろ,都道府県の切片がランダムではなく,単に異なると仮定する方が自然かも知れない。
Hausman検定であれ他の検定であれ,間違う確率は存在する。以下では間違った場合どうなるかを考えた。
\(\text{Cov}\left(a_ix_{it}\right)= 0\),即ち,REモデルが正しい場合:
誤差項の自己相関があるが,FE推定量は不偏性を満たす
\(\text{Cov}\left(a_ix_{it}\right)\neq 0\),即ち,FEモデルが正しい場合:
GM仮定4が満たされないため,RE推定量は不偏性を満たさない
Pros for RE
FEの場合,時間に対して変化しない変数の係数を推定できない
回帰式が非線形の場合(例えば,Probit),FEでは対応できない。
(結論)一般的にFEの方が適切な場合が多いのではないか。
シミュレーション#
(目的)真のモデルでは観察単位の固定効果がある場合を考え,FE推定量とRE推定量を比較する。
単回帰を想定する。以下を真の値として設定する。
b0 = 1 # 定数項
b1 = 2 # スロープ係数
推定値の計算#
シミュレーションの基本パラメータ等の設定
N = 100 # 観察単位の数
T = 5 # 時間数
ai = np.linspace(0,10,N) # 観察単位の異質性
forループによるDataFrameの作成。
df_sim = pd.DataFrame() # 空のDataFrame
for (idx,a) in enumerate(ai):
x = norm.rvs(a,1,size=T) # T個のaが平均となるランダムな数
u = norm.rvs(0,1,size=T) # 誤差項
y = b0 + b1*x + a + u # 被説明変数
df_idx = pd.DataFrame({'id':[idx]*T, # 観察個体のID
'time':np.array(range(T))+2000,
'Y':y,
'X':x,
'ai':[a]*T})
df_sim = pd.concat([df_sim,df_idx])
DataFrameの微調整。
# id と time の列を 整数型に変換(省いても問題ない)
df_sim['id'] = df_sim['id'].astype(int)
df_sim['time'] = df_sim['time'].astype(int)
# MultiIndex化
df_sim = df_sim.set_index(['id','time'])
df_sim.head()
| Y | X | ai | ||
|---|---|---|---|---|
| id | time | |||
| 0 | 2000 | -0.556991 | -0.674367 | 0.0 |
| 2001 | 6.630349 | 3.156982 | 0.0 | |
| 2002 | 0.748514 | -0.228299 | 0.0 | |
| 2003 | -0.925473 | -1.308839 | 0.0 | |
| 2004 | 0.739050 | -0.910697 | 0.0 |
固定効果モデルによる推定。
form_sim_fe = 'Y ~ X + EntityEffects'
sim_fe = PanelOLS.from_formula(form_sim_fe, data=df_sim).fit()
print(sim_fe.summary.tables[1])
Parameter Estimates
==============================================================================
Parameter Std. Err. T-stat P-value Lower CI Upper CI
------------------------------------------------------------------------------
X 1.9712 0.0525 37.512 0.0000 1.8678 2.0745
==============================================================================
ランダム効果モデルによる推定。
form_sim_re = 'Y ~ 1 + X'
sim_re = RandomEffects.from_formula(form_sim_re, data=df_sim).fit()
print(sim_re.summary.tables[1])
print('theta:', sim_re.theta.iloc[0,:].values)
Parameter Estimates
==============================================================================
Parameter Std. Err. T-stat P-value Lower CI Upper CI
------------------------------------------------------------------------------
Intercept 1.8361 0.1481 12.395 0.0000 1.5451 2.1272
X 2.8402 0.0251 113.14 0.0000 2.7909 2.8895
==============================================================================
theta: [0.26378777]
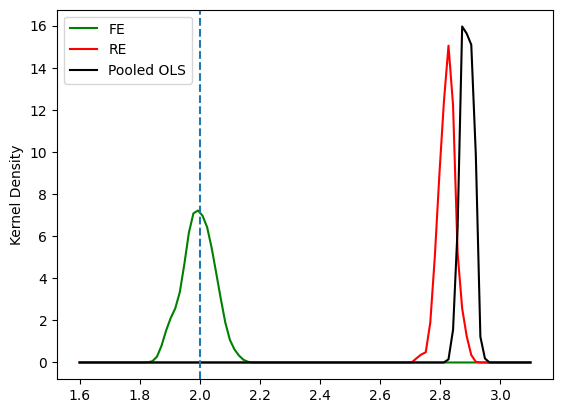
\(\text{Cov}\left(a_i,x_{it}\right)>0\)により上方バイアスが発生している。
相関ランダム効果モデルによる推定。
まず,観察単位のXの平均の列を追加する。
df_sim = add_col_mean(df_sim, 'X', 'X_mean')
form_sim_cre = 'Y ~ 1 + X + X_mean'
sim_cre = RandomEffects.from_formula(form_sim_cre, data=df_sim).fit()
print(sim_cre.summary.tables[1])
Parameter Estimates
==============================================================================
Parameter Std. Err. T-stat P-value Lower CI Upper CI
------------------------------------------------------------------------------
Intercept 1.1365 0.1227 9.2656 0.0000 0.8955 1.3774
X 1.9712 0.0525 37.541 0.0000 1.8680 2.0743
X_mean 1.0099 0.0566 17.832 0.0000 0.8986 1.1212
==============================================================================
通常のOLS(Pooled OLS)による推定はバイアスが発生する。
form_sim_pool = 'Y ~ 1 + X'
sim_pool = PooledOLS.from_formula(form_sim_pool, data=df_sim).fit()
print(sim_pool.summary.tables[1])
Parameter Estimates
==============================================================================
Parameter Std. Err. T-stat P-value Lower CI Upper CI
------------------------------------------------------------------------------
Intercept 1.5416 0.1186 12.997 0.0000 1.3085 1.7746
X 2.8995 0.0203 142.91 0.0000 2.8596 2.9394
==============================================================================
推定値の分布#
基本的に上のシミュレーションのコードを応用する。
N = 100 # 観察単位数
T = 5 # 年数
R = 100 # シミュレーションの回数
ai = np.linspace(0,10,N) # 観察単位の異質性
(下のコードについて)
ランダム効果モデルの推定には
linearmodelsを使っている。固定効果モデルと通常のOLS推定にもlinearmodelsを使うと必要がない統計量も計算するため計算に時間が掛かる。少しでも計算時間を縮めるために「手計算」をする。
bhat_fe_list = [] # FE推定値を入れるための空のリスト
bhat_re_list = [] # RE推定値を入れるための空のリスト
bhat_pool_list = [] # Pooled OLS推定値を入れるための空のリスト
for _ in range(R): # Rの値は下のコードで使わないので"_"に設定する
df = pd.DataFrame() # 空のDataFrame
# データの生成
for (idx,a) in enumerate(ai):
x = norm.rvs(a,1,size=T) # T個のaが平均となるランダムな数
u = norm.rvs(0,1,size=T) # T個の誤差項
y = b0 + b1*x + a + u # T個の被説明変数
df_idx = pd.DataFrame({'id':[idx]*T, # DataFrameへ表の追加
'time':np.array(range(T))+2000,
'Y':y,
'X':x,
'ai':[a]*T})
df = pd.concat([df,df_idx])
# RE推定
df_re = df.set_index(['id','time']) # MultiIndex化
form_sim_re = 'Y ~ 1 + X'
sim_re = RandomEffects.from_formula(form_sim_re, data=df_re).fit()
bhat_re_list.append(sim_re.params.iloc[1])
# FE推定
df_fe = df.loc[:,['Y','X']] - df.groupby('id')[['Y','X']].transform('mean')
Yfe = df_fe.loc[:,'Y'].values
Xfe = df_fe.loc[:,'X'].values[:,None] # [:,None]は(N*T,1)の行列に変換
bhat_fe = (np.linalg.inv(Xfe.T@Xfe)@Xfe.T@Yfe)[0]
bhat_fe_list.append(bhat_fe)
# Pooled OLS推定
c = np.ones(N*T)
Xpool = np.stack([c, df.loc[:,'X'].values], axis=1)
Ypool = df.loc[:,'Y'].values
bhat_pool = (np.linalg.inv(Xpool.T@Xpool)@Xpool.T@Ypool)[1]
bhat_pool_list.append(bhat_pool)
分布の図示
xx=np.linspace(1.6,3.1,num=100) # 図を作成するために横軸の値を設定
kde_model_fe=gaussian_kde(bhat_fe_list) # FE推定量のカーネル密度関数を計算
kde_model_re=gaussian_kde(bhat_re_list) # RE推定量のカーネル密度関数を計算
kde_model_pool=gaussian_kde(bhat_pool_list) # Pooled OLS推定量のカーネル密度関数を計算
plt.plot(xx, kde_model_fe(xx), 'g-', label='FE') # FE推定量の分布プロット
plt.plot(xx, kde_model_re(xx),'r-', label='RE') # RE推定量の分布プロット
plt.plot(xx, kde_model_pool(xx),'k-', label='Pooled OLS') # RE推定量の分布プロット
plt.axvline(x=b1,linestyle='dashed') # 真の値での垂直線
plt.ylabel('Kernel Density') # 縦軸のラベル
plt.legend() # 凡例
pass
標準誤差の問題#
(式3)の固定効果モデルを考えよう。パネル・データの場合,次の2つの問題が発生する場合がある。
残差の不均一分散
固定効果モデルは,変数の変換後に通常のOLS推定をおこなうため,残差に不均一分散が存在するかも知れない。(不均一分散を参照。)
残差の相関
直観的に説明するために次の例を考えよう。賃金のパネル・データを作成する際に,まず複数の会社をランダムに抽出し,それらの会社から複数の労働者をランダム抽出することにより,各労働者の時系列データを収集するとしよう。パネル・データ分析をすると次の残差の相関が発生する可能性がある。
<個体内での残差の相関> 労働者Aさんを考えよう。理想的な仮定の下では,Aさんの残差は時系列的に独立となる。しかし,その仮定が満たされない場合,Aさんの残差には自己相関が存在することになる。Bさんも,Cさんも,,,Zさんにも同様のことが言える。このタイプの相関は,個体内での期間をまたがる残差の相関である。
<個体間での残差の相関> ある期間を考えよう。会社Firm0で働くA0さん,B0さん,C0さん,,,Z0さんは,同じ会社で働いているため共通の特徴があり,残差は相関するかも知れない。別の会社Firm1で働くA1さん,B1さん,C1さん,,,Z1さんも,同様に残差は相関する可能性がある。このタイプの相関は,期間内での個体間の残差の相関となる。
これらの問題が発生しても,基本的な仮定の下(特に,GM仮定4が満たされない場合で詳しく検討するガウス・マルコフ定理4が満たされる場合)でFE推定量は不偏性と一致性を満たす。しかし,係数の標準誤差は有効ではなくなり検定が無効となる。その対処方法として,linearmodelsには主に次の2つの方法が用意されている。
不均一分散頑健推定
詳しくは,不均一分散を参照。
クラスター頑健推定
クラスターとは何らかの特徴を共有する観測値がグループ化された集まりである。クラスター頑健推定では,(1)残差の不均一分散と(2)格クラスター内での残差の相関の両方を考慮した頑健推定となる。(2)には上で説明した次のパターンが挙げられる。
個体内での残差の自己相関であり,時系列的な相関に該当する。
個体間での残差の相関であり,クロス・セクションの相関に該当する。
以下では,この2つの頑健推定の使い方を説明する。
分散の確認#
linearmodelsには残差の均一分散を調べるBreusch-Pagan検定やWhite検定をおこなうメソッドは用意されていない。ここではstatsmodelsを使いWooldridge (2016,p.253)で説明されているWhite検定に基づく検定をおこなう。次に必要な変数を作成する。
# 残差
u_hat = result_fe.resids.values.flatten()
# 被説明変数の予測値
y_hat = result_fe.fitted_values.values.flatten()
# DataFrameの作成
df_white = pd.DataFrame({'u_hat':u_hat,'y_hat':y_hat})
(上のコードの説明)
residsは残差をDataFrameとして取得する属性fitted_valuesは予測値をDataFrameとして取得する属性valuesはDataFrameをarrayとして返す属性flatten()はarrayが2次元になっているのを1次元に変換するメソッドarray([[..],[..],...[...]])をarray([....])に変換する。
検定に使う式
\(\text{H}_0:\beta_1=\beta_2=0\)(均一分散)
\(\text{H}_A:\)帰無仮説は成立しない
form_white = 'I(u_hat**2) ~ y_hat + I(y_hat**2)'
res_white = smf.ols(form_white, data=df_white).fit()
print(res_white.summary().tables[1])
print('F検定のp値:',res_white.f_pvalue)
=================================================================================
coef std err t P>|t| [0.025 0.975]
---------------------------------------------------------------------------------
Intercept 0.1172 0.010 11.249 0.000 0.097 0.138
y_hat -0.0205 0.048 -0.428 0.668 -0.114 0.073
I(y_hat ** 2) -0.0550 0.099 -0.557 0.577 -0.248 0.138
=================================================================================
F検定のp値: 0.4354339447406286
帰無仮説は棄却できない。
次に図を使い確認する。
b0 = res_white.params.iloc[0] # beta0
b1 = res_white.params.iloc[1] # beta1
b2 = res_white.params.iloc[2] # beta2
xx = np.linspace(min(y_hat), max(y_hat), 100) # x軸の値
z = b0 + b1*xx + b1*xx**2 # 検定に使った式
plt.scatter(y_hat, u_hat**2) # u_hat, y_hatの散布図
plt.plot(xx, z, 'red', linewidth=3) # 検定の式の曲線
plt.xlabel('y_hat')
plt.ylabel('u_hat^2')
pass
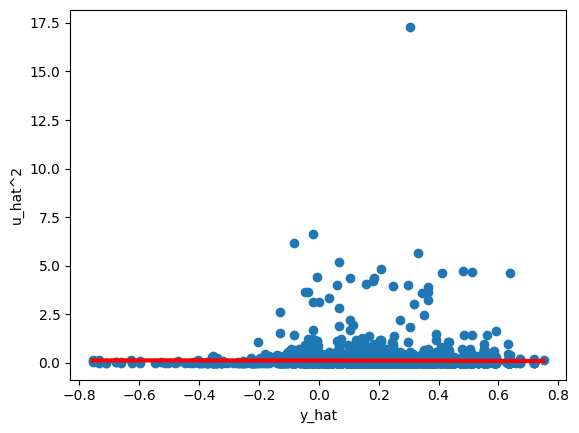
(解説)
上の検定で推定した式は赤い線である。殆ど平行になっているため帰無仮説を棄却できなかった。
図の中で
y_hatの値が-0.2を境にu_hatの変動はより大きくなっており,不均一分散の疑いが高い。
Note
残差の自己相関の検定については後日追加する予定。
対処方法#
説明と計算#
<不均一分散頑健的推定の使い方>
メソッド
fit()に以下の引数を指定する。クラスター頑健推定を指定:
cov_type='robust'
<クラスター頑健的推定の使い方>
メソッド
fit()に以下の引数を指定する。クラスター頑健推定を指定:
cov_type='clustered'グループ化するクラスターを指定:
個体のクラスターを指定する場合:
cluster_entity=True時間のクラスターを指定する場合:
cluster_time=True個体と時間の2次元のクラスターを指定する場合:
cluster_entity=True及びcluster_time=True
クラスター数が小さい場合の影響を調整する:
group_debias=True(デフォルトはFalseだが,Trueを推奨する)
(注意)
係数の推定値は変わらない。
係数の標準誤差だけが修正され,有効な検定ができるようになる。
wagepanを使って上で推定した式にクラスター頑健的推定を使う。
<不均一分散頑健的推定の場合>
mod_fe_clus1 = PanelOLS.from_formula(formula_fe, data=wagepan)
res_fe_clus1 = mod_fe_clus1.fit(cov_type='robust')
print(res_fe_clus1.summary.tables[1])
Parameter Estimates
==============================================================================
Parameter Std. Err. T-stat P-value Lower CI Upper CI
------------------------------------------------------------------------------
married 0.0467 0.0181 2.5766 0.0100 0.0112 0.0822
union 0.0800 0.0195 4.1015 0.0000 0.0418 0.1182
expersq -0.0052 0.0007 -7.8012 0.0000 -0.0065 -0.0039
d81 0.1512 0.0269 5.6182 0.0000 0.0984 0.2040
d82 0.2530 0.0275 9.2034 0.0000 0.1991 0.3069
d83 0.3544 0.0319 11.099 0.0000 0.2918 0.4171
d84 0.4901 0.0395 12.423 0.0000 0.4128 0.5675
d85 0.6175 0.0478 12.905 0.0000 0.5237 0.7113
d86 0.7655 0.0589 13.002 0.0000 0.6501 0.8809
d87 0.9250 0.0698 13.243 0.0000 0.7881 1.0620
==============================================================================
<クラスター頑健推定の場合>
mod_fe_clus1 = PanelOLS.from_formula(formula_fe, data=wagepan)
res_fe_clus1 = mod_fe_clus1.fit(cov_type='clustered',
cluster_entity=True,
group_debias=True)
print(res_fe_clus1.summary.tables[1])
Parameter Estimates
==============================================================================
Parameter Std. Err. T-stat P-value Lower CI Upper CI
------------------------------------------------------------------------------
married 0.0467 0.0210 2.2227 0.0263 0.0055 0.0879
union 0.0800 0.0227 3.5180 0.0004 0.0354 0.1246
expersq -0.0052 0.0008 -6.4007 0.0000 -0.0068 -0.0036
d81 0.1512 0.0256 5.9147 0.0000 0.1011 0.2013
d82 0.2530 0.0287 8.8269 0.0000 0.1968 0.3092
d83 0.3544 0.0349 10.169 0.0000 0.2861 0.4228
d84 0.4901 0.0455 10.783 0.0000 0.4010 0.5792
d85 0.6175 0.0568 10.871 0.0000 0.5061 0.7288
d86 0.7655 0.0712 10.746 0.0000 0.6258 0.9052
d87 0.9250 0.0840 11.006 0.0000 0.7602 1.0898
==============================================================================
不均一分散頑健推定とクラスター頑健推定の係数の標準誤差(従って,t値)は異なる。理由は,残差にある個体ごとの自己相関の存在である。実際,残差の自己相関AR(1)を検定すると,その存在を棄却できない。従って,不均一分散頑健推定は自己相関を取りこぼすことになり,標準誤差が小さくなっている。
Note
固定効果モデルを使いクラスター頑健推定について説明したが,ランダム効果モデルや通常の回帰分析でも使うことができる。例えば,通常の回帰分析の場合は次のコードとなる。
formula = 'lwage ~ 1 + married + union + expersq \
+d81+d82+d83+d84+d85+d86+d87'
mod = PooledlOLS.from_formula(formula, data=wagepan)
res = mod.fit(cov_type='clustered',
cluster_entity=True,
group_debias=True)
クラスター頑健推定の妥当性は,データの収集プロセスなどを考慮して検討する必要があるだろう。
Warning
クラスター頑健推定について次の点に注意しよう。
大標本(\(N\rightarrow\infty\))の下で有効となる。
個体数が十分に大きい必要がある。個体数が小さい場合に使うと,問題を悪化させる可能性がある。
個体数よりも時系列のデータが長いパネル・データの場合は意味がない推定となってしまう。
p値について#
一方で,linearmodelsでクラスター頑健推定を使う場合,p値の計算については以下で説明する点について覚えておくと良いだろう。次の変数を定義しよう。
\(n\):各個体の観測値
\(G\): 個体数(クラスターの数,GroupのG)
\(N=nG\): 標本の大きさ
\(k\): 定数項以外の説明変数の数
linearmodelsは,クラスター頑健推定のp値を計算する際,t分布に自由度N-G-kを使っている。変数marriedを使って,数値で確認してみる。N-G-kは推定結果のオブジェクトres_fe_clus1の属性.df_residかる抽出することができる。
# 自動計算のp値
pval_auto_calc = res_fe_clus1.pvalues['married']
# 「手計算」のp値
dof = res_fe_clus1.df_resid # 自由度
pval_manual_calc = 2*(
1-t.cdf(res_fe_clus1.tstats['married'], dof) )
print('marreidのp値\n'+'-'*27)
print(f'自動計算: {pval_auto_calc}')
print(f'「手動計算」:{pval_manual_calc}')
marreidのp値
---------------------------
自動計算: 0.02629288992739931
「手動計算」:0.02629288992739931
同じ値だということが分かる。
一方,Stata(xtregコマンド)では,この場合の自由度はG-1を使っている。この値を使ってp値を計算し直して比較してみよう。推定結果のオブジェクトres_fe_clus1の属性entity_infoは,個体に関する情報をSeriesとして返す。
res_fe_clus1.entity_info
mean 8.0
median 8.0
max 8.0
min 8.0
total 545.0
Name: Observations per entity, dtype: float64
データセットはbalanced dataset(\(n_1=n_2=\cdots=n_G\))であり,それぞれの個体には8の観測値があることが分かる。またtotalは個体の総数を表しているので,次の変数を作成しよう。
G = int( res_fe_clus1.entity_info['total'] )
# Stataで使う自由度
dof_stata = G-1
この値を使いp値を計算してみよう。
2 * ( 1-t.cdf(res_fe_clus1.tstats['married'], dof_stata) )
0.026644617992753306
小数点第3位まではlinearmodelsと同じ値だが,それ以降はStataの結果と異なる。Stataの結果とは,若干異なる事を覚えておくと,後になって戸惑うことを避けることができるだろう。
では,どちらを使えば良いのだろうか。Stataが使う自由度\(G-1\)の方が一般的であるため,その慣例に従えば良いだろう。一方で,自由度が30以上のt分布の場合,標準正規標分布との誤差は非常に小さな値になる。両方の自由度を表示してみる。
print(f'linearmodelsの自由度:{dof}')
print(f'Stataの自由度:{dof_stata}')
linearmodelsの自由度:3805
Stataの自由度:544
2つのケースとも,自由度は大きいため,上の計算が示すように,p値の差は大きくない。実際に,標準正規分布を使った場合のp値を計算してみよう。
2 * ( 1-norm.cdf(res_fe_clus1.tstats['married']) )
0.02623433711762968
近い値になっていることが分かる。従って,手元のデータが\(N\rightarrow\infty\)と近似でき,且つ,個体数\(G\)が十分に大きいと判断される場合は,次のように使い分けるのも一案だろう。
暫定的な推定には,
linearmodelsのデフォルトのp値を使い,最終盤の推定式を模索する。卒論などの提出版には,自由度\(G-1\)とする
p値を「手計算」する。
いずれlinearmodelsも変更するかもしれないが,現状では,この方法が最も現実的だろう。

