操作変数法と2段階OLS#
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import wooldridge
from linearmodels.iv import IV2SLS
from scipy.stats import chi2, gaussian_kde, multivariate_normal, norm, uniform
# 警告メッセージを非表示
import warnings
warnings.filterwarnings("ignore")
<仮定4が満たされない場合>
説明#
基本的な考え方#
仮定4:Zero Conditional Mean \(\text{E}(u|x)=0\)
仮定4a:\(\text{Cov}(x,u)=0\)
この仮定が満たされない理由に次の3つがあり(他にもある),その対処法となる推定方法について説明する。
欠落変数
同時方程式
測定誤差
この仮定4もしくは4aが満たされている場合,\(x\)は外生変数という。一方,この仮定が満たされない場合,OLS推定量は不偏性も一致性も満たさない。その場合の説明変数は内生変数とよばれる。説明変数の内生性は経済問題に多く存在すると考えられる。例えば,既出の賃金関数を考えよう。賃金は教育や経験などに依存しているが,労働者の内在的な能力にも依存していると考えられる。能力を捉える変数が回帰式にない場合(欠落変数),その効果は誤差項\(u\)に入ることになる。もちろん,能力が労働者の中でランダムに存在し,仮定4もしくは4aを満たしているのであれば問題がない。しかし説明変数である教育が誤差項に含まれる能力と何らかの関係がある場合(例えば,能力の高い人がより高い教育水準を選択する),仮定4もしくは4aは満たされないことになり,OLS推定量は不偏性を満たさない(欠落変数バイアスがある)。
Note
内生変数とは誤差項と相関する変数を意味する。従って,被説明変数も内生変数である。しかし,以下では「内生変数」という用語を「内生的説明変数」の省略形として使うことにする。
このような場合に役に立つのが操作変数法(Instrumental Variable Estimation)と呼ばれる手法である。この推定法では,ある条件を満たす内生変数の代わりになる操作変数(外生変数)を使うことにより,一致性を満たす推定量を得ることが可能となる。
(注意点)
IV推定量は一致性を満たすが,この特性を活かすためには十分に大きな標本が必要である。
標本の大きさが小さい場合,IV推定量は不偏性を失う。
OLS推定量と比べてIV推定量の標準誤差は大きくなる(効率性が低い)。
基本的なアイデアを整理するために次の単回帰式を考えよう。
\(w\)は説明変数
\(\text{Cov}(w,u)\neq 0\)(即ち,\(w\)は内生変数)
<操作変数の3つの条件>
更に,\(w\)に以下の条件を満たす操作変数(instruments)\(z\)があるとしよう。
\(z\)は回帰式に含まれない(除外条件)
\(\text{Cov}(z,w)\neq 0\)(妥当性; \(w\)と高い相関関係がある)
\(\text{Cov}(z,u)=0\)(外生性; 回帰式の誤差項と無相関)
この場合,操作変数法を用いて(大標本のもとで)一致性を満たす\(\hat{\beta}_1\)を得ることが可能となる。
<推定方法の考え方>
操作変数(IV)推定方は2段階最小2乗法の特殊なケースとして理解できる。
操作変数の数と内生変数の数が等しい場合の推定法を操作変数(IV)推定法
操作変数の数が内生変数の数を上回る場合の推定法を2段階最小二乗法(2 Stage Least Squares; 2SLS)
第1段階OLS
次式をOLS推定する。
これにより\(w\)を予測値\(\hat{w}\)と残差\(\hat{v}\)に分解する。
(4)#\[ w=\hat{w}+\hat{v},\qquad\hat{w}=\hat{\pi}_0+\hat{\pi}_1z \]\(\hat{w}\)(予測値):外生変数で説明できる\(w\)の部分(\(z\)と相関する部分)
\(\hat{v}\)(残差):残り全て(\(u\)と相関する\(w\)の部分は\(\hat{v}\)に吸収される)
\(\hat{\pi}_1\)の統計的優位性の確認
一般的に有効な操作変数は以下を満たす
操作変数の\(t\)値の絶対値 \(>3.2\)
この目安を満たさなければ弱操作変数の可能性があり,その場合,推定量は不偏性・一致性を満たさない
帰無仮説\(\text{H}_0:\;\hat{\pi}_1=0\)が棄却され,上の基準をクリアすれば次のステップへ
第2段階OLS
予測値\(\hat{w}\)を使い次式をOLS推定する。
(5)#\[ y=\gamma_0+\gamma_1\hat{w}+e \]\(\hat{\gamma}_1\):IV(instrumental variable)推定量
(注意点)
「手計算」で第1・2段階を別々にOLS推定すると,\(\hat{\gamma}_j\)を得ることができるが,推定量の標準誤差,検定統計量,決定係数\(R^2\)は有効ではない。
Pythonの専用パッケージを使と,大標本のもとで推定量と\(t\)値は有効となる。
\(R^2\)は特に有用な情報を提供しない(マイナスになり得る)。
パラメータ制約を検定する\(F\)検定をする場合は「手計算」ではなくパッケージで提供されたコマンドを使うこと。
linearmodels#
<linearmodelsの使い方>
回帰式を文字列で表し操作変数法を使うためにはサブパッケージIV2SLSのfrom_formulaをインポートする。回帰式の文字列に関して上述した定数項についての違い以外はstatsmodelsと同じである。ただし,下の回帰式の一般型に沿って内生変数と操作変数を~で挟んで[ ]の中に入れる。
<IV2SLS回帰式の一般形>
被説明変数 ~ 定数項 + 外生変数 + [内生変数 ~ 操作変数]
定数項,外生変数がない場合は省いても良い。
[ ]がない場合は通常のOLSとして計算される。その際,以前説明したメソッドfit()のオプションに要注意。外生変数,操作変数は複数でも可
ケース1:単純なIV推定#
データ#
既婚女性の教育の収益率に関するデータmrozを利用して使い方を説明する。
mroz = wooldridge.data('mroz').dropna(subset=['lwage']) # 列'lwage'にNaNがある行は削除する
wooldridge.data('mroz',description=True)
name of dataset: mroz
no of variables: 22
no of observations: 753
+----------+---------------------------------+
| variable | label |
+----------+---------------------------------+
| inlf | =1 if in lab frce, 1975 |
| hours | hours worked, 1975 |
| kidslt6 | # kids < 6 years |
| kidsge6 | # kids 6-18 |
| age | woman's age in yrs |
| educ | years of schooling |
| wage | est. wage from earn, hrs |
| repwage | rep. wage at interview in 1976 |
| hushrs | hours worked by husband, 1975 |
| husage | husband's age |
| huseduc | husband's years of schooling |
| huswage | husband's hourly wage, 1975 |
| faminc | family income, 1975 |
| mtr | fed. marg. tax rte facing woman |
| motheduc | mother's years of schooling |
| fatheduc | father's years of schooling |
| unem | unem. rate in county of resid. |
| city | =1 if live in SMSA |
| exper | actual labor mkt exper |
| nwifeinc | (faminc - wage*hours)/1000 |
| lwage | log(wage) |
| expersq | exper^2 |
+----------+---------------------------------+
T.A. Mroz (1987), “The Sensitivity of an Empirical Model of Married
Women’s Hours of Work to Economic and Statistical Assumptions,”
Econometrica 55, 765-799. Professor Ernst R. Berndt, of MIT, kindly
provided the data, which he obtained from Professor Mroz.
ケース1では以下の場合を考える。
被説明変数:
lwage(既婚女性の賃金; 対数)内生変数:
educ(既婚女性の教育年数)操作変数:
fatheduc(父親の教育年数)外生的説明変数:なし
(考え方)
誤差項に既婚女性の能力が含まれている可能性があるためeducは内生変数の疑いがある。父親の教育年数fatheducは既婚女性の教育年数educと正の相関性があると思われる一方,能力自体とは無相関と仮定。
自動計算#
IV推定法は2SLSの特殊なケースとして2ステップで推定することを説明したが,ここでは自動的に2ステップを計算する場合を紹介する。
まず回帰式を決める。
form_1 = 'lwage ~ 1 + [educ ~ fatheduc]'
IV2SLSモジュールのfrom_formulaを使うことにより,statsmodelsのolsのように回帰式を文字列で指定できる。次式では推定するモデルを設定する。
mod_1 = IV2SLS.from_formula(form_1, data=mroz)
statsmodelsのolsのようにメソッド.fit()を使い推定する。(以前説明したオプションについての説明を参照)
res_1 = mod_1.fit(cov_type='unadjusted')
res_1の属性.summary,さらにsummaryの属性tablesを使ってパラメータの部分だけを表示する。
print(res_1.summary.tables[1])
Parameter Estimates
==============================================================================
Parameter Std. Err. T-stat P-value Lower CI Upper CI
------------------------------------------------------------------------------
Intercept 0.4411 0.4451 0.9911 0.3216 -0.4312 1.3134
educ 0.0592 0.0351 1.6878 0.0914 -0.0095 0.1279
==============================================================================
educの推定値は,上で説明したようにfatheducを操作変数として計算した結果である。\(p\)値は0.1よりも低いため10%有意水準では係数0の帰無仮説を棄却できるが,5%水準では棄却できない。
「手計算」#
第1・2段階のOLS推定を別々に試みる。
第1段階のOLS
stage_1 = 'educ ~ 1 + fatheduc' # 回帰式
res_stage_1 =IV2SLS.from_formula(stage_1, data=mroz).fit(cov_type='unadjusted') # OLS推定
mroz['educ_fit'] = res_stage_1.fitted_values # educの予測値を取得
上の3行目のではres_stage_1の属性.fitted_valuesを使い予測値を取得している。statsmodelsを使いOLS推定した際に使った.fittedvaluesと異なるメソッド名になっていることに注意しよう。
第2段階のOLS
stage_2 = 'lwage ~ 1 + educ_fit'
res_stage_2 =IV2SLS.from_formula(stage_2, data=mroz).fit(cov_type='unadjusted') # OLS推定
print(res_stage_2.summary.tables[1])
Parameter Estimates
==============================================================================
Parameter Std. Err. T-stat P-value Lower CI Upper CI
------------------------------------------------------------------------------
Intercept 0.4411 0.4660 0.9465 0.3439 -0.4723 1.3545
educ_fit 0.0592 0.0367 1.6119 0.1070 -0.0128 0.1311
==============================================================================
「自動計算」の場合と比べると,Parameterは同じことが確認できる。しかしStd. Err.は異なり,それに基づく他の推定値も異なることに注意。
\(OLS\)推定#
確認のために,操作変数法を使わずに直接OLS推定をおこなうとどうなるかを確認しよう。
form_ols = 'lwage ~ 1 + educ'
res_ols =IV2SLS.from_formula(form_ols, data=mroz).fit() # OLS推定
print(res_ols.summary.tables[1])
Parameter Estimates
==============================================================================
Parameter Std. Err. T-stat P-value Lower CI Upper CI
------------------------------------------------------------------------------
Intercept -0.1852 0.1703 -1.0872 0.2770 -0.5191 0.1487
educ 0.1086 0.0134 8.1178 0.0000 0.0824 0.1349
==============================================================================
操作変数法の推定量と大きく異なることが分かる。操作変数法と比べてeducの\(OLS\)推定量は約2倍になり,既婚女性の教育の収益率を過大評価している。educと誤差項に相関がると推測できる。
ケース2:より複雑なIV推定(2SLS)#
説明#
ケース1を次のように拡張する。
複数の外生変数の導入(
exper,expersq)複数の操作変数の導入(
fatheduc,motheduc)
このように拡張しても基本的な考え方は同じである。
\(\text{Cov}(w,u)\neq 0\)(\(w\)は内生変数)
\(\text{Cov}(x_k,u)=0,\;k=1,2\)(\(x_k\)は外生変数)
\(w\)の操作変数\(z_j,\;j=1,2\)は次の条件を満たす必要がある。
\(\text{Cov}(z_j,w)\neq 0,\quad j=1,2\)
\(\text{Cov}(z_j,u)=0,\quad j=1,2\)
<2SLSの考え方>
第1段階OLS
次式をOLS推定する。
(7)#\[ w=\pi_0+\pi_1z_1+\pi_2z_2+\pi_3x_1+\pi_4x_2+v \]\(w\)を2つの要素(\(\hat{w}\)と\(\hat{v}\))に分解
(8)#\[ w=\hat{w}+\hat{v}, \qquad \hat{w}=\hat{\pi}_0+\hat{\pi}_1z_1+\hat{\pi}_2z_2+\hat{\pi}_3x_1+\hat{\pi}_4x_2 \]\(\hat{w}\)(予測値):外生変数だけで説明される\(w\)の部分(\(x_1\),\(x_2\),\(z_1\),\(z_2\)と相関する部分)
\(v\)(残差):残り全て(\(u\)と相関する\(w\)の部分はこれに吸収される)
\(\hat{\pi}_1\)と\(\hat{\pi}_2\)の優位性の確認
操作変数の\(F\)値 \(>10\)
この目安を満たさなければ弱操作変数の可能性
推定量は不偏性・一致性を満たさない
\(\text{H}_0:\;\hat{\pi}_1=\hat{\pi}_2=0\)が棄却され,上の基準をクリアすれば次のステップへ
第2段階OLS
予測値\(\hat{w}\)を使い次式をOLS推定する。
(9)#\[ y=\gamma_0+\gamma_1x_1+\gamma_2x_2+\gamma_3\hat{w}+e \]IV(instrumental variable)推定量:\(\hat{\gamma}_3\)
educと操作変数の相関性チェック#
内生変数と操作変数のOLS推定を使い,相関性の検定をおこなう。
上述のとおり,一般的に有効な操作変数は以下を満たす。
操作変数が1つの場合
操作変数の\(t\)値の絶対値 \(>3.2\)
複数の操作変数の場合
操作変数の\(F\)値 \(>10\)
form_check = 'educ ~ 1 + fatheduc + motheduc'
res_check =IV2SLS.from_formula(form_check, data=mroz).fit(cov_type='unadjusted')
print(res_check.summary)
OLS Estimation Summary
==============================================================================
Dep. Variable: educ R-squared: 0.2081
Estimator: OLS Adj. R-squared: 0.2043
No. Observations: 428 F-statistic: 112.45
Date: Sat, Sep 20 2025 P-value (F-stat) 0.0000
Time: 00:35:01 Distribution: chi2(2)
Cov. Estimator: unadjusted
Parameter Estimates
==============================================================================
Parameter Std. Err. T-stat P-value Lower CI Upper CI
------------------------------------------------------------------------------
Intercept 9.4801 0.3200 29.627 0.0000 8.8530 10.107
fatheduc 0.1881 0.0335 5.6122 0.0000 0.1224 0.2538
motheduc 0.1564 0.0357 4.3805 0.0000 0.0864 0.2263
==============================================================================
fatheducとmotheducのそれぞれの係数T-stat(\(t\)値)\(>3.2\)P-value(\(p\)値)は約\(0\)
2つの操作変数の係数が同時に\(0\)という帰無仮説の検定
F-statistic(\(F\)値)\(>10\)P-value(F-stat)(\(t\)値)も約\(0\)
従って,educと操作変数の相関性は高い。
IV推定#
上述したIV2SLS回帰式の一般形に基づいて回帰式を設定する。
form_2 = 'lwage ~ 1 + exper + expersq +[educ ~ fatheduc + motheduc]'
操作変数法を使い推定
res_2 =IV2SLS.from_formula(form_2, data=mroz).fit(cov_type='unadjusted')
print(res_2.summary.tables[1])
Parameter Estimates
==============================================================================
Parameter Std. Err. T-stat P-value Lower CI Upper CI
------------------------------------------------------------------------------
Intercept 0.0481 0.3985 0.1207 0.9039 -0.7329 0.8291
exper 0.0442 0.0134 3.3038 0.0010 0.0180 0.0704
expersq -0.0009 0.0004 -2.2485 0.0245 -0.0017 -0.0001
educ 0.0614 0.0313 1.9622 0.0497 7.043e-05 0.1227
==============================================================================
IVが1つのケースと比べてeducの係数自体は大きく変わってはいないが,5%有意水準でも係数0の帰無仮説を棄却できるようになっている。
ケース3:複数の内生変数#
説明#
複数の内生変数がある場合を考える。まず重要なのは,各内生変数に1つ以上の操作変数が存在していることが前提となる。
以下では次の仮定の下でシミュレーションを通して推定方法を説明する。
母集団回帰式
(10)#\[ y=\beta_0+\beta_1x_1+\beta_2x_2+\beta_3x_3+\gamma_1w_1+\gamma_2w_2+e \]誤差項\(e\)は全ての説明変数と無相関
\(w_1\)は\(x_1\)と,\(w_2\)は\(x_2\)とそれぞれ相関する。
\(\text{Cov}(w_1,x_1)=0.5\)
\(\text{Cov}(w_2,x_2)=0.5\)
説明変数の他の共分散は全て
0とする。
\(x_1\)と\(x_2\)は欠落変数として次の回帰式を推定する。
(11)#\[ y_i=\beta_0+\beta_3x_{i3}+\gamma_1w_{i1}+\gamma_2w_{i2}+u_i \]\(u_i=e+\beta_1x_{i1}+\beta_2x_{i2}\)
\(x_{i3}\)は外生変数
\(w_{i1}\)は内生変数,即ち,\(\text{Cov}(w_{i1},u_i)=\text{Cov}(w_{i1},x_{i1})\neq0\)
\(w_{i2}\)は内生変数,即ち,\(\text{Cov}(w_{i2},u_i)=\text{Cov}(w_{i2},x_{i2})\neq0\)
\(w_{ij}\)の操作変数は\(z_{ij}\),\(j=1,2\)とする。
\(\text{Cov}(z_{ij},w_{ij})=0.8\neq 0\)(妥当性)
\(\text{Cov}(z_{ij},u_i)=0\)(外生性)
ここでガウス・マルコフ定理の仮定4が満たされない理由は,欠落変数\(x_1\)と\(x_2\)の存在である。
内生変数が複数あっても推定の基本的な考え方は変わらない。違いは,第1段階において内生変数の数だけ(この例では2回)OLS推定をする必要がある点のみである。
第1段階OLS
次の2式をOLS推定する。
\[\begin{split} \begin{align*} w_1&=a_{0}+a_{1}z_1+a_{2}z_2+a_{3}x_3+v_1\\ w_2&=b_{0}+b_{1}z_1+b_{2}z_2+b_{3}x_3+v_2 \end{align*} \end{split}\]それぞれを予測値\(\hat{w}_j\)と残差\(\hat{v}_j\)に分解する。
\[\begin{split} \begin{align*} w_j&=\hat{w}_j+\hat{v}_j,\quad j=1,2\\ \hat{w}_1&=\hat{a}_{0}+\hat{a}_{1}z_1+\hat{a}_{2}z_2+\hat{a}_{3}x_3\\ \hat{w}_2&=\hat{b}_{0}+\hat{b}_{1}z_1+\hat{b}_{2}z_2+\hat{b}_{3}x_3 \end{align*} \end{split}\]\(\hat{w}_j\)(予測値):外生変数で説明できる\(w_j\)の部分
\(\hat{v}_j\)(残差):残り全て(\(u\)と相関する\(w\)の部分は\(\hat{v}_j\)に吸収される)
\(\hat{a}_{1}\)と\(\hat{b}_{2}\)の統計的優位性の確認
一般的に有効な操作変数は以下を満たす
操作変数の\(t\)値の絶対値 \(>3.2\)
この目安を満たさなければ弱操作変数の可能性があり,その場合,推定量は不偏性・一致性を満たさない
帰無仮説 \(\text{H}_0:\;\hat{a}_{1}=\hat{b}_{2}=0\)が棄却され,上の基準をクリアすれば次のステップへ
第2段階OLS
予測値\(\hat{w}_j\),\(j=1,2\),を使い次式をOLS推定する。
\[ y=\mu_0+\mu_1\hat{w}_1+\mu_2\hat{w}_2+\mu_3x_3+\varepsilon \]\(\hat{\mu}_1\)と\(\hat{\mu}_2\):IV(instrumental variable)推定量
データの作成#
まずデータを作成するが,真のパラメターの値を次のように仮定する。
データの大きさはn_sampleとする。
n_sample = 10_000
# x1, x2, x3, w1, w2, z1, z2の平均
rv_mean = [0, 0, 0, 0, 0, 0, 0]
# 共分散行列 x1, x2,x3, w1, w2, z1, z2
rv_cov = [[ 1, 0, 0,0.5, 0, 0, 0], # x1
[ 0, 1, 0, 0,0.5, 0, 0], # x2
[ 0, 0, 1, 0, 0, 0, 0], # x3
[0.5, 0, 0, 1, 0,0.8, 0], # w1
[ 0,0.5, 0, 0, 1, 0,0.8], # w2
[ 0, 0, 0,0.8, 0, 1, 0], # z1
[ 0, 0, 0, 0,0.8, 0, 1]] # z2
# ランダム変数の生成
rv = multivariate_normal.rvs(rv_mean, rv_cov, size=n_sample)
# 説明変数と操作変数の抽出
x1 = rv[:,0] # 外生変数(欠落)
x2 = rv[:,1] # 外生変数(欠落)
x3 = rv[:,2] # 外生変数
w1 = rv[:,3] # 内生変数
w2 = rv[:,4] # 内生変数
z1 = rv[:,5] # 操作変数
z2 = rv[:,6] # 操作変数
# yの生成
y = 1 + x1 + x2 + x3 +w1 + w2 + np.random.normal(size=n_sample)
# DataFrameの作成
var_dict = {'y':y,'x1':x1,'x2':x2,'x3':x3,'w1':w1,'w2':w2,'z1':z1,'z2':z2}
df_endog2 = pd.DataFrame(var_dict)
上のコードにより,df_endog2にシミュレーションで使用するデータが割り当てられている。最初の3行を表示してみよう。
df_endog2.head(3)
| y | x1 | x2 | x3 | w1 | w2 | z1 | z2 | |
|---|---|---|---|---|---|---|---|---|
| 0 | -4.745284 | -0.296030 | -1.150557 | 0.528224 | -1.422186 | -1.053908 | -1.478837 | -0.846954 |
| 1 | 3.676835 | 0.641440 | 0.562289 | 0.490720 | 0.351650 | 0.940325 | 0.527298 | 1.221438 |
| 2 | -0.292302 | -0.995481 | -0.710800 | 1.620217 | -0.755902 | -0.846454 | -0.649801 | -0.139534 |
最小二乗法による推定#
formula_0 = 'y ~ w1 + w2 + x3'
print(IV2SLS.from_formula(formula_0, data=df_endog2).fit().summary.tables[1])
Parameter Estimates
==============================================================================
Parameter Std. Err. T-stat P-value Lower CI Upper CI
------------------------------------------------------------------------------
Intercept 1.0113 0.0157 64.358 0.0000 0.9805 1.0421
w1 1.4947 0.0155 96.127 0.0000 1.4642 1.5252
w2 1.5080 0.0157 95.899 0.0000 1.4772 1.5389
x3 0.9760 0.0157 62.107 0.0000 0.9452 1.0068
==============================================================================
欠落変数と相関がない\(x_3\)の係数の推定値は真の値である1に近い。一方,欠落変数と相関する\(w_1\)と\(w_2\)は真の値1から大きく外れていることが確認できる。
「手計算」#
第1段階OLS#
2つの推定式
formula_1 = 'w1 ~ z1 + z2 + x3'
formula_2 = 'w2 ~ z1 + z2 + x3'
両方の推定式にz1とz2が入っていることに留意しよう。上述のようにx3が両式に入る理由と同じ効果を捉えるためである。
OLS推定
res_endog2_1 = IV2SLS.from_formula(formula_1, data=df_endog2).fit()
res_endog2_2 = IV2SLS.from_formula(formula_2, data=df_endog2).fit()
print(res_endog2_1.summary.tables[1])
Parameter Estimates
==============================================================================
Parameter Std. Err. T-stat P-value Lower CI Upper CI
------------------------------------------------------------------------------
Intercept 0.0041 0.0060 0.6813 0.4957 -0.0077 0.0158
z1 0.7932 0.0060 132.35 0.0000 0.7815 0.8050
z2 0.0070 0.0059 1.1823 0.2371 -0.0046 0.0185
x3 -0.0035 0.0060 -0.5730 0.5666 -0.0153 0.0084
==============================================================================
z1の係数の推定値である\(\hat{\gamma}_1\)の\(t\)値\(>3.2\)であり,w1の操作変数としての妥当性は満たしている。
print(res_endog2_2.summary.tables[1])
Parameter Estimates
==============================================================================
Parameter Std. Err. T-stat P-value Lower CI Upper CI
------------------------------------------------------------------------------
Intercept 0.0165 0.0060 2.7497 0.0060 0.0047 0.0282
z1 -0.0045 0.0060 -0.7621 0.4460 -0.0162 0.0071
z2 0.7961 0.0060 132.03 0.0000 0.7843 0.8079
x3 -0.0022 0.0060 -0.3738 0.7086 -0.0139 0.0095
==============================================================================
z2の係数の推定値である\(\hat{\gamma}_2\)の\(t\)値\(>3.2\)であり,w2の操作変数としての妥当性を満たしている。
次に,それぞれの残差をdf_endog2に新たな列w1hatとw2hatとして追加する。
df_endog2['w1hat'] = res_endog2_1.fitted_values
df_endog2['w2hat'] = res_endog2_2.fitted_values
第2段階OLS#
推定式を定義する。
formula_12 = 'y ~ w1hat + w2hat + x3'
推定結果の表示
print(IV2SLS.from_formula(formula_12, data=df_endog2).fit().summary.tables[1])
Parameter Estimates
==============================================================================
Parameter Std. Err. T-stat P-value Lower CI Upper CI
------------------------------------------------------------------------------
Intercept 1.0316 0.0238 43.324 0.0000 0.9849 1.0782
w1hat 0.9810 0.0299 32.782 0.0000 0.9223 1.0396
w2hat 1.0337 0.0297 34.770 0.0000 0.9754 1.0919
x3 0.9794 0.0237 41.287 0.0000 0.9329 1.0259
==============================================================================
全ての推定値が真の値である1に概ね近いことが分かる。
自動計算#
linearmodelsのIV2SLSを使うが,次の書き方となる。
被説明変数 ~ 定数項 + 外生変数 + [内生変数1 + 内生変数2 ~ 操作変数1 + 操作変数2]
定数項,外生変数がない場合は省いても良い。
外生変数,操作変数は複数でも可
推定式を定義しよう。
formula_2 = 'y ~ 1 + x3 + [w1 + w2 ~ z1 + z2]'
推定結果を表示する。
print(IV2SLS.from_formula(formula_2, data=df_endog2).fit().summary.tables[1])
Parameter Estimates
==============================================================================
Parameter Std. Err. T-stat P-value Lower CI Upper CI
------------------------------------------------------------------------------
Intercept 1.0316 0.0172 59.966 0.0000 0.9979 1.0653
x3 0.9794 0.0172 56.991 0.0000 0.9457 1.0131
w1 0.9810 0.0215 45.670 0.0000 0.9389 1.0231
w2 1.0337 0.0217 47.699 0.0000 0.9912 1.0761
==============================================================================
推定値は「手計算」の結果と同じであることが確認できる。「手計算」の標準誤差とは異なるが,必ず自動計算の値を使うように!
シミュレーション:3つの特徴#
一致性#
(目的)
IV推定量の一致性を確認する。
<シミュレーションの内容>
母集団の説明変数には
x1とx2があり,x2を欠落変数とする単回帰分析。(12)#\[ y=\beta_0 + \beta_1 x_1 + u \]zをx1の操作変数とする。2つの推定方法
操作変数
zを使いIV法による推定OLSによる推定(この場合,欠落変数バイアスが発生する)
標本の大きさは
1000,標本数(ループの回数)を10000として\(\hat{\beta}_1\)の分布を比べる
標本数(ループの回数)
N = 10_000
母集団のパラメータ
b0 = 0.5
b1 = 1
b2 = 0.5
シミュレーションの関数を設定する。
引数
n:標本の大きさm:x1とzの共分散 \(\text{Cov}(x_1,z)=m\)ols(デフォルトはFalse):OLS推定を一緒に行う場合はTrue
返り値
IV推定値のリスト(
ols=False)IV推定値のリストとOLS推定値のリスト(
ols=True)
(コメント)
計算の速度を早めるために下の関数の中ではIV2SLSは使わずnumpyの関数を使いIVとOLS推定値を計算している。IV2SLSは係数の推定値だけではなく他の多くの統計値も自動的に計算するために一回の計算に比較的に長い時間を要するためである。
def sim_iv(n, m, ols=False): # n=標本の大きさ, m=x1とzの共分散
"""
n: 標本の大きさ
m: 説明変数と対応する操作変数の相関性の度合い
ols: Boolean(デフォルト:False)
False: OLS推定とIV推定も一緒におこなう
返り値:2つのリスト(OLSとIV推定量)
True: IV推定のみ
返り値:1つのリストのみ
"""
rv_mean = [0, 0, 0] # x1, x2, z1の平均
rv_cov = [[1.0, 0.3, m], # x1, x2, z1の共分散行列
[0.3, 1.0, 0.0], # 全ての変数の分散は1(対角成分)
[m, 0.0, 1.0]] # Cov(x1,x2)=0.3, Cov(x2,z)=0, Cov(x1,z)=m,
rv = multivariate_normal.rvs(rv_mean, rv_cov, size=n) # x1, x2, z1をnセット抽出
x1 = rv[:,0] # 説明変数
x2 = rv[:,1] # 欠落変数
z = rv[:,2] # 操作変数
b1_iv_list = [] # IV推定量を入れる空のリスト
b1_ols_list = [] # OLS推定量を入れる空のリスト
c = np.ones(n)
for j in range(N): # N回のループ
u = norm.rvs(size=n) # 母集団の誤差項
y = b0 + b1*x1 + b2*x2 + u # 母集団回帰式
# IV 第1ステージ
Xiv1 = np.stack([c,z],axis=1)
pihat = np.linalg.inv((Xiv1.T)@Xiv1)@(Xiv1.T)@x1 # IV推定
x1hat = Xiv1@pihat # x1の予測値
# IV 第2ステージ
Xiv2 = np.stack([c,x1hat],axis=1)
beta_iv = np.linalg.inv((Xiv2.T)@Xiv2)@(Xiv2.T)@y # IV推定
b1_iv_list.append(beta_iv[1]) # IV推定量をリストに追加
if ols==True: # オプションols=Trueの場合はOLS推定もおこなう
X = np.stack([c,x1],axis=1)
beta_ols = np.linalg.inv((X.T)@X)@(X.T)@y # OLS推定
b1_ols_list.append(beta_ols[1]) # OLS推定量をリストに追加
else: # ols=Falseの場合はOLS推定をおこなわない
pass
if ols==True: # ols=True の場合の返り値の設定
return b1_iv_list, b1_ols_list
else: # ols=False の場合の返り値の設定
return b1_iv_list
シミュレーションの開始
b1hat_iv, b1hat_ols = sim_iv(1000, 0.9, ols=True)
図示
xx=np.linspace(0.8, 1.3, num=100) # 図を作成するために横軸の値を設定
kde_model_ols=gaussian_kde(b1hat_ols) # OLS推定量のカーネル密度関数を計算
kde_model_iv=gaussian_kde(b1hat_iv) # IV推定量のカーネル密度関数を計算
plt.plot(xx, kde_model_ols(xx), 'g-', label='OLS') # OLS推定量の分布プロット
plt.plot(xx, kde_model_iv(xx), 'r-', label='IV') # IV推定量の分布プロット
plt.axvline(x=b1, linestyle='dashed')
plt.ylabel('Kernel Density') # 縦軸のラベル
plt.legend() # 凡例
pass
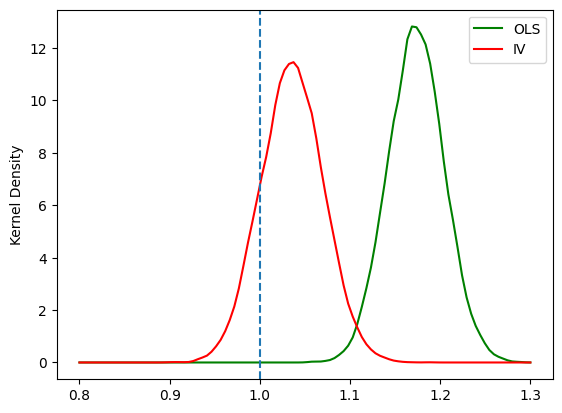
欠落変数が発生しているため
OLS推定量は一致性は満たさない。IV推定量は一致性を満たす。
標本の大きさ#
(目的)
IV推定量の一致性は大標本特性である。ここでは標本の大きさの効果を確認する。
<シミュレーションの内容>
上と同じ設定
IV法による単回帰分析のみを考える標本の大きさを
30,100,1000それぞれ
N=10000回推定し\(\hat{\beta}_1\)の分布を比べる
上で使った関数sim_iv()をデフォルト(ols=False)で使う。
b1hat_iv_30 = sim_iv(30,0.8)
b1hat_iv_100 = sim_iv(100,0.8)
b1hat_iv_1000 = sim_iv(1000,0.8)
図示
xx=np.linspace(0.5, 1.5, num=100) # 図を作成するために横軸の値を設定
b1hat_iv_n_list = [b1hat_iv_30, b1hat_iv_100, b1hat_iv_1000]
color_list = ['g-', 'r-', 'k-']
label_list = ['n=30', 'n=100', 'n=1000']
for (i, j, k) in zip(b1hat_iv_n_list, color_list, label_list):
kde_model_iv=gaussian_kde(i) # IV推定量のカーネル密度推定を設定
b1_dist = kde_model_iv(xx) # IV推定量のカーネル密度関数を計算
plt.plot(xx, b1_dist, j, label=k) # IV推定量の分布プロット
plt.axvline(x=b1, linestyle='dashed')
plt.ylabel('Kernel Density') # 縦軸のラベル
plt.legend() # 凡例
pass
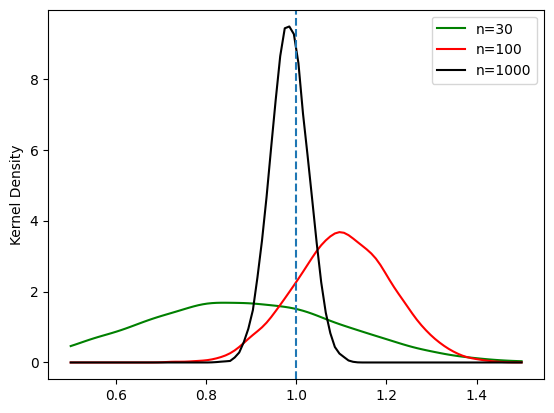
標本の大きさが増加すると,分散は低下する。
標本の大きさが小さい場合,不偏性は満たされないこともわかる。
操作変数との相関性(弱操作変数)#
(目的)
IV推定法で必須となるのが内生変数と操作変数の相関である。相関が高い場合は推定量の標準誤差は低くなるが,逆に相関が低い場合は推定量の標準誤差が大きくなることを確認する。
<シミュレーションの内容>
上と同じ設定
IV法による単回帰分析のみを考える内生変数と操作変数の共分散
mを0.1,0.4,0.8の3つのケースを考える。標本の大きさ\(2000\)に固定し,それぞれ
N=10000回推定し\(\hat{\beta}_1\)の分布を比べる
上で使った関数sim_iv()を使う。
シミュレーションの開始
b1hat_iv_weak = sim_iv(2000,0.1)
b1hat_iv_mid = sim_iv(2000,0.4)
b1hat_iv_strong = sim_iv(2000,0.8)
図示
xx=np.linspace(0.5,1.5,num=100) # 図を作成するために横軸の値を設定
b1hat_iv_n_list = [b1hat_iv_weak, b1hat_iv_mid, b1hat_iv_strong]
color_list = ['g-', 'r-', 'k-']
label_list = ['Cov(x1,z)=0.1', 'Cov(x1,z)=0.4', 'Cov(x1,z)=0.8']
for (i, j, k) in zip(b1hat_iv_n_list, color_list, label_list):
kde_model_iv=gaussian_kde(i) # OLS推定量のカーネル密度推定を設定
b1_dist = kde_model_iv(xx) # OLS推定量のカーネル密度関数を計算
plt.plot(xx, b1_dist, j, label=k) # OLS推定量の分布プロット
plt.axvline(x=b1,linestyle='dashed')
plt.ylabel('Kernel Density') # 縦軸のラベル
plt.legend() # 凡例
pass
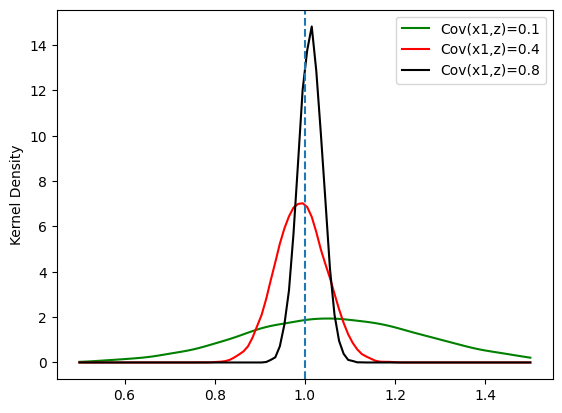
\(\text{Cov}(x,z)\)が低くなると分散が大きくなり,一致性を失うことも確認できる。
説明変数の外生性の検定#
説明#
次式を考えよう。
\(\text{Cov}(w,u)=0\)の場合,
OLSがより良い推定量OLS推定量は不偏性・一致性を満たす。IV-2SLS推定量一致性を満たすが不偏性は欠き,標準誤差が大きくなり精度を損なう。
\(\text{Cov}(w,u)\neq 0\)の場合,
IV-2SLSがより良い推定量OLS推定量は不偏性・一致性を満たさない。IV-2SLS推定量は一致性を満たす。
このように説明変数が外生的か内生的かによって推定量の性質が大きく異なる。ではIV推定法とOLS推定法のどちらを使うべきなのか。この問題は説明変数が外生的か(\(\text{Cov}(w,u)=0\))それとも内生的か(\(\text{Cov}(w,u)\neq 0\))に依存しており,ここではその検定方法について説明する。
上で考えたケース2を使って確かめる。
検定方法1:Wu-Hausman検定#
帰無仮説と対立仮説:
\(\text{H}_0:\;w\)は外生変数(\(\text{Cov}(w,u)=0\))
\(\text{H}_0:\;w\)は内生変数(\(\text{Cov}(w,u)\neq0\))
(基本的な考え方)
帰無仮説のもとでは,IV推定法もOLS推定法も一致性も満たすため
の値は小さいはず。逆に,帰無仮説が成立しない場合,OLS推定量は不偏性も一致性も失うことになり,上の値は大きくなる。即ち,上の値が大きければ(小さければ),帰無仮説を棄却できる可能性が高くなる(低くなる)。この考えを利用したのがWu-Hausman検定である。
res_2のメソッド.wu_hausman()を使うと検定統計量と\(p\)値が表示される。
(注意).wu_hausman()であって.wu_hausmanではない。
res_2.wu_hausman()
Wu-Hausman test of exogeneity
H0: All endogenous variables are exogenous
Statistic: 2.8035
P-value: 0.0948
Distributed: F(1,423)
WaldTestStatistic, id: 0x11bef43b0
\(p\)値は0.0948。5%の有意水準では帰無仮説を棄却できない(外生性を棄却できない)が,10%では棄却できる。
検定方法2#
まず検定方法について説明し,「考え方」については後述する。次の回帰式を考えよう。
\(x\)は外生変数
\(w\)は内生性が疑われる説明変数
2段階で検定する。
第1段階
式(14)のOLS残差\(\hat{u}\)を計算する。
第2段階
式(14)に\(\hat{u}\)を加えてOLS推定する。
(15)#\[y=\gamma_0+\gamma_1x + \gamma_2w+\gamma_u\hat{u}+e\qquad\qquad (\text{式2})\]次の検定をおこなう。
\(\text{H}_0:\;\hat{\gamma}_u=0\)(\(w\)は外生変数である)
\(\text{H}_A:\;\hat{\gamma}_u\neq 0\)(\(w\)は内生変数である)
(コメント)計算上\(\hat{\gamma}_i=\hat{\beta}_i,\;i=0,1,2\)が成り立つことになる。
——– 考え方 ——–
<第1段階>
(式1)を推定すると\(y\)を\(\hat{y}\)と\(\hat{u}\)に分解することができる。
\[y=\hat{y}+\hat{u}\]\(\hat{y}\):説明変数で説明できる\(y\)の部分
\(\hat{u}\):\(y\)のその他の部分
\(u\)が\(w\)と相関していれば,その相関する部分が\(\hat{u}\)に含まれることになる。次のようなイメージ。
\[\hat{u}=a\hat{u}_w+bv,\qquad a,b\ne 0\]\(\hat{u}_w\):\(w\)と相関する部分
\(v\):\(w\)と相関しない部分
<第2段階>
式(15)を推定すると,相関部分である\(\hat{u}_w\)を\(\gamma_u\hat{u}\)として取り出すことができる。
もし\(\gamma_u\)が有意であれば,\(\text{H}_0\)は棄却され,\(\hat{u}_w\)は存在するということになり\(w\)は内生変数と判断できる。
もし\(\gamma_u\)が有意でなければ,\(\text{H}_0\)は棄却できない。\(\hat{u}_w\)は存在しないということになり,\(w\)は外生変数と判断できる。
「手計算」#
第1段階
form_2a = 'educ ~ 1 + exper + expersq + motheduc + fatheduc'
mod_2a = IV2SLS.from_formula(form_2a, data=mroz)
res_2a = mod_2a.fit(cov_type='unadjusted')
第2段階
res_2aの残差を使うが,メソッドresidsを使い取得する。すなわち,res_2a.residsが残差を返す。また次の点も覚えておこう。
res_2a.residsを直接回帰式に入れることはできないが,I()の引数とすれば可能となる。これはstatsmodelsと同じである。
form_2b = 'lwage ~ 1 + educ + exper + expersq + I(res_2a.resids)'
mod_2b = IV2SLS.from_formula(form_2b, data=mroz)
res_2b = mod_2b.fit(cov_type='unadjusted')
print(res_2b.summary.tables[1])
Parameter Estimates
====================================================================================
Parameter Std. Err. T-stat P-value Lower CI Upper CI
------------------------------------------------------------------------------------
Intercept 0.0481 0.3923 0.1226 0.9024 -0.7207 0.8169
educ 0.0614 0.0308 1.9932 0.0462 0.0010 0.1218
exper 0.0442 0.0132 3.3559 0.0008 0.0184 0.0700
expersq -0.0009 0.0004 -2.2840 0.0224 -0.0017 -0.0001
I(res_2a.resids) 0.0582 0.0346 1.6810 0.0928 -0.0097 0.1260
====================================================================================
\(p\)値は0.0928で,5%の有意水準では帰無仮説を棄却できない(内生性を棄却できない)。
自動計算#
linearmodelsには上の計算を自動でおこなった結果を示すメソッドが用意されている。res_2の.wooldridge_regressionである。
res_2.wooldridge_regression
Wooldridge's regression test of exogeneity
H0: Endogenous variables are exogenous
Statistic: 2.8256
P-value: 0.0928
Distributed: chi2(1)
WaldTestStatistic, id: 0x11bf9fbc0
(注意)「手計算」で使った.fit()のオプションdebiased=Trueを使うと異なる数値になる。
操作変数の妥当性検定(過剰識別制約検定)#
説明#
次の回帰式を考えよう。
\(x\):外生変数
\(w\):内生性が疑われる説明変数
<ケース1:1つの内生変数に1つの操作変数がある場合>
\(z\):操作変数
この場合,操作変数の外生性\(\text{Cov}(z,u)=0\)が満たされないといけないが,これを検定できない。
(理由)
式(16)の
wは内生性が疑われるため,その式を使い計算したOLS残差\(\hat{u}\)は真の誤差項を捉えていない可能性がある。従って,この\(\hat{u}\)を使っても意味がある検定とはならない。式(16)に\(z\)を使い残差を計算することも考えられるが,そもそも\(z\)の妥当性が分からないため,これも真の誤差項を捉えていない可能性がある。
この場合,経済理論に基づいて操作変数の外生性を正当化できるかが問題になる。
<ケース2:1つの内生変数に複数の操作変数がある場合>
2つの操作変数\(z_1\)と\(z_2\)
この場合,同時に\(\text{Cov}(z_1,u)=\text{Cov}(z_2,u)=0\)が成立するかを検定する方法があり,その1つがSargan検定と呼ばれる。
(注意)
Sargan検定は,全ての操作変数(上の例では2つ)が同時に妥当かどうかを検定する。言い換えると,同時に妥当ではない場合は,次のパターンとなる。
\(z_1\)は妥当だが,\(z_2\)は妥当ではない。
\(z_1\)は妥当ではないが,\(z_2\)は妥当である。
\(z_1\)と\(z_2\)の両変数は妥当ではない。
従って,同時に妥当ではない場合,どの操作変数が有効かを調べることはできない。
(コメント)
操作変数の数が内生変数の数を上回っているケースは「過剰識別(overidentified)」と呼ばれる。
操作変数の数と内生変数の数が等しい場合は「適度識別」(just identified)と呼ばれる。
Sargan検定は過剰識別の場合のみ意味がある検定であり,「過剰識別制約検定」の一つとなる。
Sargan検定
2段階で検定する。
第1段階
IV-2SLS推定法で推定し,残差\(\hat{u}\)を取得する。
第2段階
帰無仮説と対立仮説の設定
\(\text{H}_0:\) 全ての操作変数は妥当である(\(\hat{u}\)は全ての操作変数と相関性がなく外生的である)。
\(\text{H}_A:\) \(\text{H}_0\)は成立しない(少なくとも1つの操作変数は\(\hat{u}\)と相関する)。
上の例では,操作変数の数は
2であり内生変数の数は1であるため\(q=2-1=1\)の過剰識別制約があると考える。
\(\hat{u}\)を被説明変数として全ての外生変数と操作変数に対してOLS推定し,決定係数\(R^2\)を計算する。
\(LM\)統計量 \(=nR^2\)
\(nR^2\sim\chi(q)\)
\(q>1\)は操作変数の数と内生変数の差
\(n\)は標本の大きさ
(帰無仮説棄却の意味)
少なくとも1つの操作変数は誤差項と相関性があるということになる。(欠落変数とも解釈可能)
しかしどの操作変数が内生的かは分からない。
上で考えたケース2を使って確かめてみよう。
「手計算」#
第1段階の計算結果としてres_2を使う。
第2段階の計算のためにres_2の属性.residsを使い回帰残差を取得し,直接以下の回帰式に入れる。
form_aux = 'I(res_2.resids) ~ 1 + motheduc + fatheduc + exper + expersq' # 外生的説明変数を省いてもよい
mod_aux = IV2SLS.from_formula(form_aux, data=mroz)
res_aux = mod_aux.fit(cov_type='unadjusted')
検定統計量の計算
r2 = res_aux.rsquared # 決定係数
n = res_aux.nobs # 標本の大きさ
teststat = n * r2 # 検定統計量
pval = 1 - chi2.cdf(teststat, 1) # p値の計算
print(pval)
0.5386372330713853
5%有意水準では帰無仮説を棄却できない。
自動計算#
res_2のメソッド.sarganを使うと上と同じ計算結果を表示できる。
res_2.sargan
Sargan's test of overidentification
H0: The model is not overidentified.
Statistic: 0.3781
P-value: 0.5386
Distributed: chi2(1)
WaldTestStatistic, id: 0x11c626270
同時方程式モデルとIV推定#
同時性バイアス#
同時方程式モデルとは,均衡メカニズムなどを通して複数の内生変数が複数の式によって同時決定されるモデルである。例として労働の需給モデルを考えよう。均衡では需要量(\(L_d\))と供給量(\(L_s\))は等しくなり(\(L=L_d=L_s\)),需要と供給はそれぞれ均衡賃金(\(W\))に依存する。
供給関数
(17)#\[ L = s_0+s_1 W + s_2 X_s + u_s \]\(s_1>0\)
\(X_s=\) 供給の「その他」の決定要因(例えば,限界費用)
\(u_s=\) 供給の誤差項
需要関数
(18)#\[ W = d_0+d_1 L + d_2 X_d + u_d \]\(d_1<0\)
\(X_d=\) 需要の「その他」の決定要因(例えば,所得)
\(u_d=\) 需要の誤差項
(相関性の仮定)
\(\text{Cov}(X_s,u_s)=\text{Cov}(X_s,u_d)=0\)
\(\text{Cov}(X_d,u_d)=\text{Cov}(X_d,u_s)=0\)
\(\text{Cov}(u_s,u_d)=0\)
IV推定法の適用#
同時性バイアスはIV推定法で対処可能である。考え方は簡単である。
供給曲線式(17)の推定
\(W\)の操作変数として\(X_d\)を使う。\(X_d\)は操作変数の3つの条件を満たす。
供給曲線式(18)の推定
例#
データ#
データセットmrozを使う。
労働供給曲線:労働市場に参加する既婚女性の労働供給関数
労働需要曲線:企業が提示(オファー)する賃金をその決定要因の関数として表す
上の記号に対応する変数をリストアップする(1975年のデータ)。
\(L\):
hours(労働時間)\(W\):
lwage(賃金時間額の対数)\(X_s\):労働供給の外生変数
age(年齢)kidslt6(子どもが6歳未満)nwifeinc:((家計の所得 - 賃金*時間)/1000)
\(X_d\):賃金オファーの外生変数
exper(雇用経験)expersq(雇用経験の2乗)
両方に含まれる変数:
educ(教育年数)
供給曲線の推定#
IV推定
form_L = 'hours ~ 1 + educ + age + kidslt6 + nwifeinc + [lwage ~ exper + expersq]'
mod_L = IV2SLS.from_formula(form_L, data=mroz)
res_L = mod_L.fit(cov_type='unadjusted')
print(res_L.summary.tables[1])
Parameter Estimates
==============================================================================
Parameter Std. Err. T-stat P-value Lower CI Upper CI
------------------------------------------------------------------------------
Intercept 2225.7 570.52 3.9011 0.0001 1107.5 3343.9
educ -183.75 58.684 -3.1312 0.0017 -298.77 -68.733
age -7.8061 9.3120 -0.8383 0.4019 -26.057 10.445
kidslt6 -198.15 181.64 -1.0909 0.2753 -554.17 157.86
nwifeinc -10.170 6.5682 -1.5483 0.1215 -23.043 2.7039
lwage 1639.6 467.27 3.5088 0.0005 723.73 2555.4
==============================================================================
OLS推定
form_L_ols = 'hours ~ 1 + educ + age + kidslt6 + nwifeinc + lwage '
mod_L_ols = IV2SLS.from_formula(form_L_ols, data=mroz)
res_L_ols = mod_L_ols.fit(cov_type='unadjusted')
print(res_L_ols.summary.tables[1])
Parameter Estimates
==============================================================================
Parameter Std. Err. T-stat P-value Lower CI Upper CI
------------------------------------------------------------------------------
Intercept 1523.8 303.43 5.0219 0.0000 929.07 2118.5
educ -6.6219 17.989 -0.3681 0.7128 -41.879 28.636
age 0.5623 5.1039 0.1102 0.9123 -9.4411 10.566
kidslt6 -328.86 100.74 -3.2643 0.0011 -526.31 -131.40
nwifeinc -5.9185 3.6574 -1.6182 0.1056 -13.087 1.2500
lwage -2.0468 54.494 -0.0376 0.9700 -108.85 104.76
==============================================================================
2つの推定結果を比べると,推定値を含めて大きく異なることがわかる。2段回推定法により同時性バイアスを取り除いた結果と解釈できる。
需要曲線の推定#
IV推定
form_P = 'lwage ~ 1 + educ + exper + expersq + [hours ~ age + kidslt6 + nwifeinc]'
mod_P = IV2SLS.from_formula(form_P, data=mroz)
res_P = mod_P.fit(cov_type='unadjusted')
print(res_P.summary.tables[1])
Parameter Estimates
==============================================================================
Parameter Std. Err. T-stat P-value Lower CI Upper CI
------------------------------------------------------------------------------
Intercept -0.6557 0.3358 -1.9527 0.0509 -1.3139 0.0024
educ 0.1103 0.0154 7.1488 0.0000 0.0801 0.1406
exper 0.0346 0.0194 1.7847 0.0743 -0.0034 0.0726
expersq -0.0007 0.0005 -1.5634 0.1179 -0.0016 0.0002
hours 0.0001 0.0003 0.4974 0.6189 -0.0004 0.0006
==============================================================================
OLS推定
form_W_ols = 'lwage ~ 1 + educ + exper + expersq + hours'
mod_W_ols = IV2SLS.from_formula(form_W_ols, data=mroz)
res_W_ols = mod_W_ols.fit(cov_type='unadjusted')
print(res_W_ols.summary.tables[1])
Parameter Estimates
==============================================================================
Parameter Std. Err. T-stat P-value Lower CI Upper CI
------------------------------------------------------------------------------
Intercept -0.4620 0.2027 -2.2797 0.0226 -0.8592 -0.0648
educ 0.1062 0.0141 7.5400 0.0000 0.0786 0.1338
exper 0.0447 0.0133 3.3590 0.0008 0.0186 0.0708
expersq -0.0009 0.0004 -2.1883 0.0286 -0.0016 -8.96e-05
hours -5.655e-05 4.353e-05 -1.2992 0.1939 -0.0001 2.876e-05
==============================================================================
労働供給の推定結果と比べて,パラメータの推定値の変化は大きくないが,統計的優位性は大きく変化している。
測定誤差とIV推定#
測定誤差によるバイアス#
ここではシミュレーションを通して,測定誤差バイアスがある場合でもIV推定法を使うことで一致性を満たす推定量を得ることが可能であることを示す。
次の母集団回帰式を考えよう。
ここで,被説明変数\(y\)は正確に測定できるが,説明変数\(x^*\)は以下の式に従って測定される仮定する。
\(x\):測定値
\(e\):測定誤差
(仮定)
測定誤差\(e\)は真の値と無関係。即ち,\(\text{Cov}(x^*,e)=0\)
(結果)
次式をOLS推定する場合,\(\hat{\beta}_1\)は不偏性・一致性を満たさない。
(理由)
仮定4:\(\text{Cov}(x,u)=0\)が満たされない。
IV推定法の適用#
IV推定法での対処方法を考える。\(x^*\)を測定する変数\(z\)があるとする。
\(v\sim\text{iid}(0,\sigma)\)は誤差であり,\(\text{iid}\)は独立同一分布を意味する。
IV推定
\(x\)の操作変数として\(z\)を使う
以下の条件を満たすと仮定する。
もとの式に含まれていない。
\(\text{Cov}(v,u)=0\;\;\Rightarrow\;\;\text{Cov}(z,u)=0\)
\(\text{Cov}(z,x)\neq 0\)(\(z\)も\(x\)も\(x^*\)を測定する変数)
シミュレーション#
(目的)
測定誤差によるバイアスを示す。
IV推定法により一致性が成立することを示す。
<シミュレーションの内容>
単回帰分析
(23)#\[ y=\beta_0 + \beta_1 x + u \]2つのケース
\(OLS\)推定
\(IV\)推定
それぞれのケースで標本の大きさ\(n=100\)
1000回推定し\(\hat{\beta}_1\)の分布を比べる
標本の大きさと標本数(ループの回数)
n = 1000
N = 10_000
母集団のパラメータの真の値
b0 = 1.0
b1 = 1.0
x_pop = uniform.rvs(1,10,size=n) # 母集団の説明変数
u = norm.rvs(scale=1, size=n) # 母集団の誤差項
y = b0 + b1*x_pop + u # 母集団回帰式
測定誤差の標準偏差
error_sd = 3
シミュレーション開始
# シミュレーションで計算した推定量を入れる空のリストの作成
b1_ols_list = [] # OLS推定量
b1_iv_list = [] # IV推定量
for j in range(N): # N回のループ
x = x_pop + norm.rvs(scale=error_sd, size=n) # 測定誤差
z = x_pop + norm.rvs(scale=error_sd, size=n) # 操作変数
c = np.ones(n) # 定数項
# IV 第1ステージ
Xiv1 = np.stack([c,z],axis=1)
pihat = np.linalg.inv((Xiv1.T)@Xiv1)@(Xiv1.T)@x # IV推定
xhat = Xiv1@pihat # x1の予測値
# IV 第2ステージ
Xiv2 = np.stack([c,xhat],axis=1)
beta_iv = np.linalg.inv((Xiv2.T)@Xiv2)@(Xiv2.T)@y # IV推定
b1_iv_list.append(beta_iv[1]) # b1のIV推定量をリストに追加
# OLS
X = np.stack([c,x],axis=1)
beta_ols = np.linalg.inv((X.T)@X)@(X.T)@y # OLS推定
b1_ols_list.append(beta_ols[1]) # b1のOLS推定量
結果の図示
xx=np.linspace(0.4,1.2,num=100) # 図を作成するために横軸の値を設定
kde_model_ols=gaussian_kde(b1_ols_list) # t値のカーネル密度推定を設定
b1_ols_dist = kde_model_ols(xx)
kde_model_iv=gaussian_kde(b1_iv_list) # t値のカーネル密度推定を設定
b1_iv_dist = kde_model_iv(xx)
plt.plot(xx, b1_ols_dist, 'g-', label='OLS Estimates') # t値の分布プロット
plt.plot(xx, b1_iv_dist,'r-', label='IV Estimates') # t分布
plt.axvline(x=b1,linestyle='dashed')
plt.ylabel('Kernel Density') # 縦軸のラベル
plt.legend()
pass
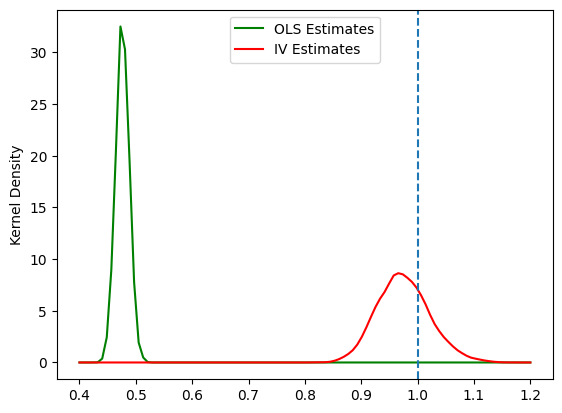
OLS推定量は不偏性も一致性も満たさない。
IV推定量は一致性を満たす。

