制限従属変数モデル#
import japanize_matplotlib
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import statsmodels.formula.api as smf
import py4macro
import wooldridge
from py4etrics.truncreg import Truncreg
from py4etrics.tobit import Tobit
from py4etrics.heckit import Heckit
from py4etrics.hetero_test import het_test_probit
from scipy.stats import norm
# 警告メッセージを非表示
import warnings
warnings.filterwarnings("ignore")
説明#
制限従属変数(Limited Dependent Variables; LDV)とは,被説明変数が取り得る値が大きく制限される場合を指す。LogitとProbitも制限従属変数の例であり,被説明変数は\((0,1)\)に制限されている。この章では,違ったタイプの制限従属変数を考える。
データの性質上2つに分けることができる。
切断データ(Truncated Data)
特定のデータが標本に含まれていない。
例:平成30年度「環境にやさしい企業行動調査」の調査対象企業は,従業員数500名以上となっており,500名未満の企業は含まれていない。
打ち切りデータ(Censored Data)
端点解の場合
募金の金額の例:募金しない場合は0円だが,募金する人の額は正の値を取る。(下からの打ち切りデータ)
データ制約の場合
所得調査の例:X万円からY万円のようにカテゴリーでまとめる場合が通常であり,最高額カテゴリーはZ万円以上のようになる。この場合,Z万円以上の所得は全てZ万円となる。(上からの打ち切りデータ)
(コメント)以下のようにも呼ばれる
下からの打ち切りデータ = 左からの打ち切りデータ(left-censored)
上からの打ち切りデータ = 右からの打ち切りデータ(right-censored)
データの性質に分けて次のモデルの使い方を説明する。
切断回帰モデル(Truncated Regression):切断データ
Tobitモデル:打ち切りデータ
Heckitモデル:切断データで選択バイアス問題が発生する場合
切断回帰モデル#
説明#
無作為な形ではなく,ある特定の一部のデータが標本から欠落している切断データの分析を考える。例として,女性の労働供給を考えよう。
\(\cal{Y}\):観測されたデータの集合(通常,無作為に選択されないと考える)。
\(\cal{N}\):観測されないデータの集合(通常,無作為に選択されないと考える)。
\(x\):労働供給に関する決定要因(例えば,教育年数)
\(u|x\sim \text{Normal}(0,\sigma^2)\):労働供給に関するランダムな要素(例えば,好み)
\(x\)を所与とすると,\(u\)は正規分布に従う。
この仮定が非常に重要であり計算の前提となる。
\(y_i\):実際の労働供給(非負の連続変数)
<結果>
標本集合\(\cal{Y}\)は無作為標本ではない。従って,GM仮定2が満たされないためOLS推定量\(\hat{\beta}_{\text{ols}}\)は不偏性を満たさない。また一致性も満たさない。
まずシミュレーションを使ってこの結果を直感的に確認する。
シミュレーション#
# 標本の大きさ
n = 100
# y*を決定するx
x = np.sort(norm.rvs(0,3,size=n)) # ランダム変数を生成し昇順に並べる
# 被説明変数
y = 1 + x + norm.rvs(0,3,size=n)
# DataFrame
df = pd.DataFrame({'Y':y, 'Y_trunc':y, 'X':x})
# 閾値
left = 0
# 切断データの作成
cond = (df.loc[:,'Y'] <= left)
df.loc[cond,'Y_trunc'] = np.nan
# 切断された被説明変数
y_trunc = df['Y_trunc']
ここでnp.nanとはNumPyの定数であり,欠損値NaNを示す。condの条件にある閾値left=0以下のデータは欠損値として設定されている。NumPyには次の定数もあるのでこの機会に紹介する。
np.nan:NaNnp.inf:(正の)無限np.e:\(e=2.71...\)np.pi:\(\pi=3.14...\)
母集団回帰式
formula_full = 'Y ~ X'
result_full= smf.ols(formula_full, data=df).fit()
b0_full,b1_full = result_full.params
result_full.params
Intercept 0.535185
X 0.918300
dtype: float64
切断データを使ったOLS回帰
formula_trunc = 'Y_trunc ~ X'
result_trunc = smf.ols(formula_trunc, data=df).fit()
b0_trunc, b1_trunc = result_trunc.params
result_trunc.params
Intercept 3.084664
X 0.476016
dtype: float64
比較するために2つの結果を図示する。同じ図に描くために,先に切断データを整理する。
x_trunc = df.dropna(subset=['Y_trunc']).loc[:,'X'] #1
x_min = min(x_trunc) #2
x_max = max(x_trunc) #3
#1:.dropna()を使って列Y_truncから欠損値がある行を取り除き,列Xをx_trunに割り当てる。#2:x_trunの最小値をx_minに割り当てる。#3:x_trunの最大値をx_maxに割り当てる。
matplotlibを使って2つの図を重ねて図示してみよう。
#1:母集団データの散布図
plt.scatter(x, y, facecolors='none', edgecolors='gray',label=r'$y^{*}$')
#2:切断データの散布図
plt.scatter(x, y_trunc, facecolors='gray', label=r'$y$ and $y^{*}$')
# 母集団OLS
plt.plot(x, b0_full+b1_full*x, 'k', linewidth=3, label='Population: $y^*$')
# 切断回帰
plt.plot(x_trunc, b0_trunc+b1_trunc*x_trunc, 'r', lw=3,label=r'Sample: $y> 0$')
plt.xlabel('x')
plt.ylabel(r'$y$ and $y^{*}$')
plt.legend()
pass
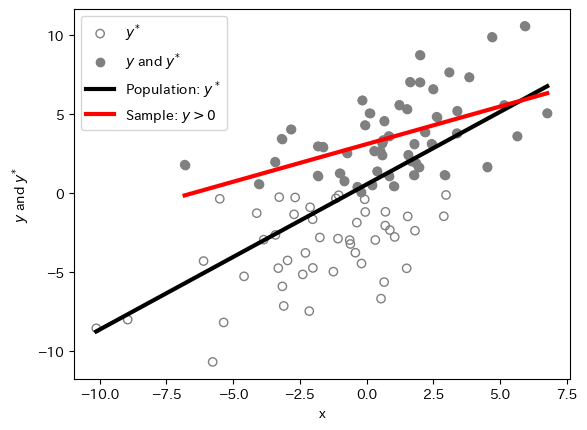
<matplotlibコードの説明>
#1:母集団データの散布図引数
facecolorsは全ての観測値の点の色を「なし」に設定する。引数
edgecolorsは全ての観測値の円周をグレーに設定する。この2つにより,全ての観測値は左下の観測値のように白抜きのグレーの円として表示される。
#1:切断データの散布図後にくる
plt.plot()は前にあるplt.plot()を上書きする。従って,切断データの観測値は母集団データの散布図上に重ねて表示されるため,引数facecolorsをgrayに設定することにより切断データだけをグレーの点として表示させることができる。
直感的な理解#
上の図を見るだけでも切断データによって引き起こされる問題をイメージすることはできるが,以下ではもう一歩踏み込んで推定量のバイアスの理由を直感的に考えてみる。
<母集団回帰>
母集団回帰式は
であり,全ての観測値を使う(即ち,切断されたデータがない)場合の条件付き期待値である母集団回帰関数(母集団で平均で成立する回帰線)は、\(\text{E}(e)=0\)の仮定の下では,次式で与えられる。
逆に言うと,(式2)に平均0の誤差項\(e\)を加えたものが母集団回帰式である。
<切断回帰>
\(y>0\)のデータだけを使う回帰式は
である。しかし,標本では\(y_i\leq 0\)のデータが切断されているため,\(y_i>0\)を考慮し\(x_i\)を所与として(式3)の期待値を取ると
となる。ここで
\(w_i\equiv\dfrac{A-(\beta_0+\beta_1x_i)}{\sigma}\)
\(A\):下限の値(この例では
0)\(\sigma_u\):誤差項の標準偏差
である。\(\sigma_u\lambda\left(w_i\right)\)の導出や\(\lambda\left(\cdot\right)\)の関数形が重要ではない。重要なのは,逆ミルズ比(inverse Mill’s ratio)と呼ばれる\(\lambda(w_i)\neq 0\)の存在であり,\(\lambda(w_i)\)は\(y>0\)となる確率の影響を捉えているという点である。従って,\(\beta_0\)と\(\beta_1\)の推定には,(式4)に残差\(\nu_i\)を追加した次式
を推定する必要がある。しかし(式3)をOLS推定すると,\(\lambda(x)\)が欠落することになり,欠落変数バイアスが発生することになる。このバイアスは,上の図で黒と赤の回帰線の傾きの違いに現れている。OLS推定量はゼロ方向にバイアスが発生する事が知られている。この問題を克服するのが切断回帰モデルである。
Truncregモジュールの使い方#
切断データを扱うために切断回帰モデルを展開する。ここでは具体的な内容は割愛するが,LogitとProbitと同じように最尤法をつかい推定する。
切断回帰モデルの推定量は一致性を満たす。
statsmodelsもlinearmodelsもTobit推定のモジュールがない。その代わりに著者が作成したpy4etricsパッケージの関数trucregモジュールを使い推定する。これはstatsmodelsのGenericMaximumLikelihoodModelを使い実装したものである。使用する上でこのサイトにある次の点に注意する必要がある。
Rの推定値と小数点第4位まで同じになるが,標準偏差は小数点第2位までが同じとなる。
Note
MacではTerminal、WindowsではGit Bashを使い、次のコマンドでpy4etricsモジュールをインストールできる。
pip install git+https://github.com/spring-haru/py4etrics.git
<使い方>
基本的にstatsmodelsのolsと同じだが,追加的な操作とオプションがある。
推定式を決める
formula = 'y ~ 1 + x'
Truncregのfrom_formulaモジュールを使って推定
Truncreg.from_formula(formula, left=<A>, right=<B>, data=<C>).fit()
ここで
left:左切断の値(デフォルトは\(-\infty\)であり,「切断なし」という意味)right:右切断の値(デフォルトは\(\infty\),「切断なし」という意味)deta:データの指定切断方向の設定:
leftだけに値を設定する場合は左切断回帰(left-truncated)となる。rightだけに値を設定する場合は右切断回帰(right-truncated)となる。leftとrightの両方に値を設定する場合は左右切断回帰(left- and right-truncated)となる。leftとrightの両方に値を設定しない場合は通常の最尤推定となる。
切断回帰推定#
例としてwooldridgeのHTVのデータを使い推定する。
htv = wooldridge.data('htv')
wooldridge.data('htv', description=True)
name of dataset: htv
no of variables: 23
no of observations: 1230
+----------+---------------------------------+
| variable | label |
+----------+---------------------------------+
| wage | hourly wage, 1991 |
| abil | abil. measure, not standardized |
| educ | highest grade completed by 1991 |
| ne | =1 if in northeast, 1991 |
| nc | =1 if in nrthcntrl, 1991 |
| west | =1 if in west, 1991 |
| south | =1 if in south, 1991 |
| exper | potential experience |
| motheduc | highest grade, mother |
| fatheduc | highest grade, father |
| brkhme14 | =1 if broken home, age 14 |
| sibs | number of siblings |
| urban | =1 if in urban area, 1991 |
| ne18 | =1 if in NE, age 18 |
| nc18 | =1 if in NC, age 18 |
| south18 | =1 if in south, age 18 |
| west18 | =1 if in west, age 18 |
| urban18 | =1 if in urban area, age 18 |
| tuit17 | college tuition, age 17 |
| tuit18 | college tuition, age 18 |
| lwage | log(wage) |
| expersq | exper^2 |
| ctuit | tuit18 - tuit17 |
+----------+---------------------------------+
J.J. Heckman, J.L. Tobias, and E. Vytlacil (2003), “Simple Estimators
for Treatment Parameters in a Latent-Variable Framework,” Review of
Economics and Statistics 85, 748-755. Professor Tobias kindly provided
the data, which were obtained from the 1991 National Longitudinal
Survey of Youth. All people in the sample are males age 26 to 34. For
confidentiality reasons, I have included only a subset of the
variables used by the authors.
<目的>
教育(educ)が賃金(wage)に与える影響を探る。1991年の時間賃金を対数化したlwageを被説明変数として使い,次の説明変数を使う。
educ:1991年までに修了した最高学位の指標abil:能力を捉える指標exper:潜在的な労働経験nc:米国北中部のダミー変数west:米国西部のダミー変数south:米国南部のダミー変数urban:都市部のダミー変数
まずOLS推定を行う。
formula_trunc = 'lwage ~ 1 + educ + abil + exper + nc + west + south + urban'
res_ols = smf.ols(formula_trunc, data=htv).fit()
print(res_ols.summary().tables[1])
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
Intercept 0.3987 0.185 2.158 0.031 0.036 0.761
educ 0.1037 0.010 10.704 0.000 0.085 0.123
abil 0.0558 0.008 6.565 0.000 0.039 0.072
exper 0.0448 0.007 6.619 0.000 0.032 0.058
nc -0.1397 0.041 -3.440 0.001 -0.219 -0.060
west -0.1282 0.049 -2.638 0.008 -0.224 -0.033
south -0.1227 0.045 -2.742 0.006 -0.210 -0.035
urban 0.2268 0.041 5.589 0.000 0.147 0.306
==============================================================================
educの係数は0.1037であり,標準誤差は0.010。
次に,wageが20以上の観測値を取り除き,20未満のサンプルだけで推計する。
htv_20 = htv.query('wage < 20') # データの抽出
print(f'切断前の標本の大きさ:{len(htv)}')
print(f'切断前の標本の大きさ:{len(htv_20)}')
print(f'削除された標本の大きさ:{len(htv)-len(htv_20)}')
切断前の標本の大きさ:1230
切断前の標本の大きさ:1066
削除された標本の大きさ:164
164のサンプルが取り除かれた。これにより,ランダムな標本ではなくなっていおり,GM仮定2が満たされていない。
res_ols_20 = smf.ols(formula_trunc,data=htv_20).fit()
print(res_ols_20.summary().tables[1])
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
Intercept 1.1795 0.174 6.795 0.000 0.839 1.520
educ 0.0579 0.009 6.258 0.000 0.040 0.076
abil 0.0548 0.008 7.168 0.000 0.040 0.070
exper 0.0218 0.006 3.467 0.001 0.009 0.034
nc -0.1373 0.038 -3.644 0.000 -0.211 -0.063
west -0.1415 0.045 -3.120 0.002 -0.230 -0.053
south -0.1176 0.042 -2.833 0.005 -0.199 -0.036
urban 0.1653 0.037 4.525 0.000 0.094 0.237
==============================================================================
educの係数は0.0579に大きく下落している。切断データをOLS推定すると(ゼロ方向に)バイアスが発生することを示している。
次に,切断回帰推定をおこなう。
右切断なので
rightに数値を設定する。説明変数が対数化されているため,それに合わせて
right=np.log(20)とする。
res_trunc = Truncreg.from_formula(formula_trunc,right=np.log(20),data=htv_20).fit()
print(res_trunc.summary().tables[1])
Optimization terminated successfully.
Current function value: 0.481943
Iterations: 1216
Function evaluations: 1715
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
Intercept 0.6094 0.302 2.018 0.044 0.017 1.201
educ 0.1060 0.017 6.312 0.000 0.073 0.139
abil 0.0818 0.013 6.448 0.000 0.057 0.107
exper 0.0356 0.011 3.309 0.001 0.015 0.057
nc -0.2552 0.068 -3.734 0.000 -0.389 -0.121
west -0.2652 0.081 -3.268 0.001 -0.424 -0.106
south -0.2078 0.074 -2.818 0.005 -0.352 -0.063
urban 0.2657 0.059 4.478 0.000 0.149 0.382
Log(Sigma) -0.5433 0.039 -14.053 0.000 -0.619 -0.468
==============================================================================
educの係数は0.1060になり,切断される前の標本をOLS推定した際の係数と近い。
(コメント)
このように切断回帰は,切断データを使いy(賃金)に対するx(教育)の効果を推定可能とする。一方で,切断されたデータの中でのyに対するxの効果に興味がある場合,バイアスが発生するため,その限界効果の絶対値は\(\left|\hat{\beta}_{\text{Truncreg}}\right|\)よりも低くなる。
<Log(Sigma)について>
誤差項は正規分布に従うと仮定され,最尤法により変数の係数\(\beta\)と誤差項の標準偏差\(\sigma\)が推定される。誤差項の標準偏差の推定値または回帰の標準偏差(
Sigma= Standard Error of Regression)の対数がLog(Sigma)である。
dir()もしくはpy4macroモジュールのsee()関数を使い推定結果res_truncの属性とメソッドを確認してみよう。
py4macro.see(res_trunc)
.aic .bic .bootstrap() .bse
.bsejac .bsejhj .conf_int() .cov_kwds
.cov_params() .cov_type .covjac .covjhj
.df_model .df_modelwc .df_resid .endog
.exog .f_test() .fitted_endog .fittedvalues
.get_nlfun() .hessv .initialize() .k_constant
.llf .llnull .llr .llr_pvalue
.load() .mle_retvals .mle_settings .model
.nobs .normalized_cov_params .params .predict()
.prsquared .pvalues .remove_data() .resid
.result_null .save() .scale .score_obsv
.set_null_options() .summary() .t_test() .t_test_pairwise()
.tvalues .use_t .wald_test() .wald_test_all_slopes
.wald_test_terms()
対数最尤関数の値
res_trunc.llf
-513.7517026401044
疑似決定係数
res_trunc.prsquared
0.17120380433327054
全ての説明変数(定数項以外)が0の場合の推定結果
print(res_trunc.result_null.summary())
Truncreg Regression Results
==============================================================================
Dep. Variable: y Pseudo R-squ: 0.000
Model: Truncreg Log-Likelihood: -619.9
Method: Maximum Likelihood LL-Null: -619.9
Date: Sat, 20 Sep 2025 LL-Ratio: -0.0
Time: 00:35:16 LLR p-value: nan
No. Observations: 1066 AIC: 1241.8
Df Residuals: 1065 BIC: 1246.7
Df Model: 0 Covariance Type: nonrobust
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
const 2.6140 0.058 44.907 0.000 2.500 2.728
Log(Sigma) -0.3590 0.047 -7.677 0.000 -0.451 -0.267
==============================================================================
検定#
次に検定方法について説明する。
Wald検定の例1
\(H_0\):定数項以外の全てのスロープ係数は0
\(H_A\):少なくとも1つの係数は0ではない
この検定のために結果のメソッドwald_test()を使うが説明変数に含まれているLog(Sigma)は残る必要がある。従って,まず定数項とLog(Sigma)以外の係数名をslopes_allに割り当てる。
slopes_all = res_trunc.model.exog_names[1:-1]
結果res_truncに属性modelがあり,その中に説明変数名の属性exog_namesを使っている。定数項と最後にくるLog(Sigma)を省くために[1:-1]を指定している。
# Wald検定
print( res_trunc.wald_test(slopes_all, scalar=True).summary() )
<Wald test (chi2): statistic=173.2213000474417, p-value=5.2528517750869245e-34, df_denom=7>
\(p\)値は非常に低いので1%の有意水準でも帰無仮説を棄却できる。
2つ目の例を考えよう。
Wald検定の例2
\(H_0\):educ+abil\(=\)exper
\(H_A\):educ+abil\(\neq\)exper
次の方法でおこなう。
制約式を文字列で設定する:
educ+abil=exper推定結果のメソッド
wald_testに制約式を引数として実行する。
print(res_trunc.wald_test('educ+abil=exper', scalar=True).summary()
)
<Wald test (chi2): statistic=130.94604539031397, p-value=2.544285617695202e-30, df_denom=1>
1%の有意水準でも帰無仮説を棄却できる。
予測値と残差#
次に2つの属性を紹介する。
.fittedvalues:以下の式で与えられる線形の予測値\[\hat{y}_i=\hat{\beta}_0+\hat{\beta}_1x_i\].resid:以下の式で与えられる線形の残差\[\hat{u}_i=y_i-\hat{y}_i\]
まず予測値の平均・最小値・最大値を計算してみる。
y_hat = res_trunc.fittedvalues
print(f'最小値:{y_hat.min()}\n平均:{y_hat.mean()}\n最大値:{y_hat.max()}')
最小値:1.436527316533825
平均:2.5085741631718674
最大値:3.556185616332395
次に残差を図示する。
u_hat = res_trunc.resid
plt.scatter(y_hat,u_hat)
plt.xlabel('y_hat')
plt.ylabel('u_hat')
pass
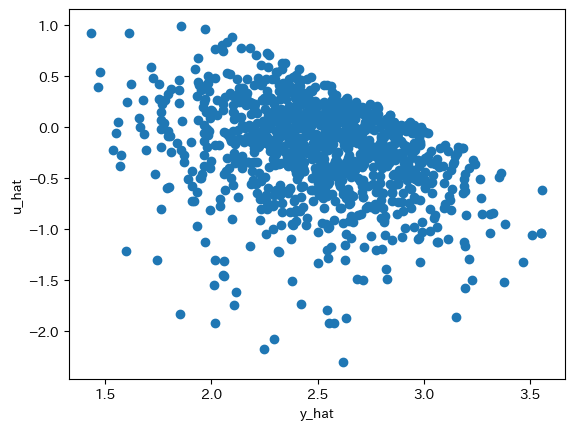
データの切断による影響が右上に見て取れる。
誤差項の仮定について#
切断回帰推定は最尤法を使っており,次の仮定が重要な役割を果たしている。
即ち,説明変数を所与とすると誤差項は正規分布に従い分散は一定であるという仮定である。
正規分布に関しての検定もあるがpy4etricsには実装されていないので,この仮定の重要性を念頭に置いて推定する必要がある。
次に不均一分散について考える。確かめるためには検定をする必要があるが,py4etricsには実装されていない。その代わりに「目安」として,通常の係数の標準偏差と不均一分散頑健標準偏差の変化を調べてみる。
# 通常の標準偏差
tr0 = res_trunc.bse
# 不均一分散頑健標準偏差
tr1 = Truncreg.from_formula(formula_trunc,
right=np.log(20),
data=htv_20).fit(cov_type='HC1',
disp=False).bse
# 不均一分散頑健標準編を使った場合の標準偏差の変化率(%)
(100*(tr1-tr0)/tr0)[:-1] # 最後は Log(Sigma) なので省く
array([ 1.31495277, 6.14965413, 2.31799016, -0.29277814, -1.99745572,
3.82073123, -3.02765197, 2.77569852])
標準偏差が減少した変数と増加したし変数がある。特別に大きくないように見えるが,これは目安であることを念頭に置いておく必要がある。
(注意)不均一分散の下での最尤推定
推定量は一致性を満たさない
標準誤差も一致性を満たさない
不均一分散頑健標準誤差を使うことが推奨されることがあるが(研究論文でもそうする研究者も多い),もともと係数の推定量が一致性を満たさないため,
cov_typeで指定する不均一分散頑健標準誤差の有用性に疑問が残る。(参照)
Tobitモデル#
説明#
打ち切りデータを理解するために,切断データと比べて異なる点を説明する。
切断データではデータセットに\((x_i,y_i),\;i\in\cal{N}\)が存在しないが,打ち切りデータには含まれる。しかし,\(y_i\)が打ち切りの下限や上限の値と等しくなる。
例として女性の労働供給を考えよう。働いている女性は多いが労働市場から退出している女性も多いのが実状である。即ち,職を持つ女性の労働供給(例えば,一週間の労働時間)は正の値をとるが,働いていない女性の労働供給は0となる。これは数式で次のように表すことができる。
\(y^{*}\):潜在変数(例えば,効用と考えても良い)
\(y^{*}>0\)の場合に実際に働き,労働供給は\(y=y^{*}\)となる。
\(y^{*}\)を効用と解釈すると,効用が正の場合,労働者は働く(\(y>0\))。その場合,効用は労働時間と同じと仮定する。(\(y=y^{*}>0\))。
\(y^{*}\leq 0\)の場合に働かないので\(y=0\)となる。
\(y^{*}\)を効用と解釈すると,効用が
0以下の場合,労働者は働かない(\(y=0\))。その場合,効用と労働時間は異なると仮定する。
\(y^{*}\)は観察不可能
\(y^{*}\)を効用と解釈すると,最もらいし仮定である。
\(x\):労働供給に関する決定要因(例えば,教育年数)
\(y\):実際の労働供給(非負の連続変数)
\(u\):労働供給に関するランダムな要素(例えば,好み)
\[u|x\sim \text{Normal}(0,\sigma^2)\]この仮定が非常に重要であり,計算の前提となる。
(コメント)
上の例では,女性が労働市場に参加するかしないかによって,\(y\)が正の値もしくは
0を取る。即ち,0が下限になっている。上限の例として,人気歌手のコンサート・チケットがあげられる。チケット数は限られており,売り切れた場合の需要は上限を上回る。また,下限・上限の両方がある場合として大学入試が挙げられる。下限はセンター試験などでの「足切り」であり,上限は定員数でる。労働供給の例では,女性の選択の結果として\(y\)の値が観察される。これはミクロ経済学でおなじみの端点解の例である。
<結果>
\(y>0\)と\(y=0\)の両方のデータを使ったOLS推定量は不偏性・一致性を満たさない。
以下ではまずこの結果をシミュレーションを使って示し,解決策について説明する。
シミュレーション#
# データの大きさ
n = 100
# y*を決定するx
x = np.sort(norm.rvs(0,3,size=n)) # ランダム変数を生成し昇順に並べる
# y*を生成
y_star = x + norm.rvs(0,3,size=n)
# yを生成
y = y_star.copy() # copy()はコピーを作るメソッド
y[y_star < 0] = 0 # y_star<0が場合,0を代入する
# DataFrame
df = pd.DataFrame({'Y':y, 'Y_star':y_star, 'X':x})
母集団回帰式は次式で与えられる。
ここで\(y^{*}\)を効用と解釈すると分かりやすいだろう。
formula_star = 'Y_star ~ X'
result_star= smf.ols(formula_star, data=df).fit()
b0_star,b1_star = result_star.params
print(result_star.params)
Intercept 0.657834
X 1.048815
dtype: float64
\(y\geq 0\)を使ったOLSの回帰式は次式となる。
ここで\(y\)は観察できる労働時間である。
formula_sample = 'Y ~ X'
result_corner = smf.ols(formula_sample, data=df).fit()
b0_corner, b1_corner = result_corner.params
print(result_corner.params)
Intercept 2.178731
X 0.554769
dtype: float64
母集団回帰式とOLS回帰の推定値は大きく異なる。図示して確かめてみよう。
# y_starの散布図
plt.scatter(x, y_star,
facecolors='none',
edgecolors='gray',
label=r'$y^{*}$')
# yの散布図
plt.scatter(x, y,
facecolors='gray',
label=r'$y$')
# 母集団OLS
plt.plot(x, b0_star+b1_star*x,
color='k',
linewidth=3,
label='潜在変数(効用): $y^*$')
# y>=0のOLS
plt.plot(x, b0_corner+b1_corner*x,
color='r',
lw=3,
label=r'観察可能なサンプル: $y\geq 0$')
plt.xlabel('x')
plt.ylabel(r'$y$ and $y^{*}$')
plt.legend()
pass
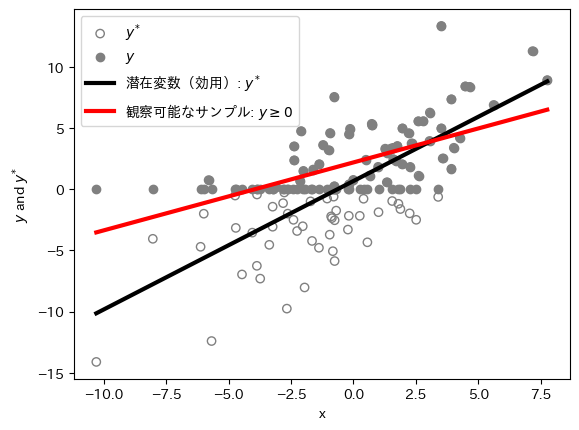
この場合,\(y\leq0\)の値を全て\(y=0\)としてOLS推定しているため,不偏性・一致性が満たされないのは直感的に理解できる。実際,上で説明したように標本回帰式は
であるが,\(y\geq 0\)の下での\(y\)の期待値 \(\text{E}(y|y>0,x)\) は複雑な非線形式なり,線形を仮定するOLS推定方で捉えることは不可能である。
Tobitモジュールの使い方#
残念ながらstatsmodelsとlinearmodelsにもTobit推定のモジュールがない。その代わりに著者が作成したpy4etricsパッケージのtobitモジュールを使い推定する。このモジュールはstatsmodelsのGenericMaximumLikelihoodModelを使い実装したものである。使用する上でこのサイトにある次の点に注意する必要がある。
Rの推定値と小数点第4位まで同じになるが,標準偏差は小数点第2位までが同じとなる。
<使い方>
基本的にstatsmodelsのolsと同じだが,追加的な操作とオプションがある。
下限・上限の設定:被説明変数
yの値に従ってNumpyのarrayもしくはPandasのSeriesを作る。下限がある場合:
-1上限がある場合:
1上限と下限の両方がない場合:
0
推定式を決める
formula = 'y ~ 1 + x'
Tobitのfrom_formulaモジュールを使って推定
Tobit.from_formula(formula, cens=<A>, left=<B>, right=<C>, data=<D>).fit()
ここで
* `cens`:ステップ1で作成した下限・上限の設定が含まれる`array`もしくは`Series`を指定する。
* `left`:下限の値(デフォルトは`0`)
* ステップ1で`-1`が設定されている場合のみ有効となる。
* `right`:上限の値(デフォルトは`0`)
* ステップ1で`1`が設定されている場合のみ有効となる。
* `deta`:データの指定
(コメント)
*LogitやProbitと同じように,非線形モデルなため最尤法を使い推定する。
Warning
censに指定するarrayの要素数,もしくはSeriesの行数が,dataで指定するDataFrameの行数と同じになる必要がある。異なる場合はエラーが発生する。必ずlen()関数を使って確認しよう!
Tobitモデルの推定#
例として、ケース1:単純なIV推定で使ったmrozのデータを使う推定を考えよう。
mroz = wooldridge.data('mroz')
女性の労働供給のモデルを考え,供給量hoursを被説明変数とする。特に,hoursは0が下限となっているためTobitモデルが妥当だと考えられる。労働時間hoursを図示してみよう。
plt.hist(mroz['hours'],bins=20)
pass
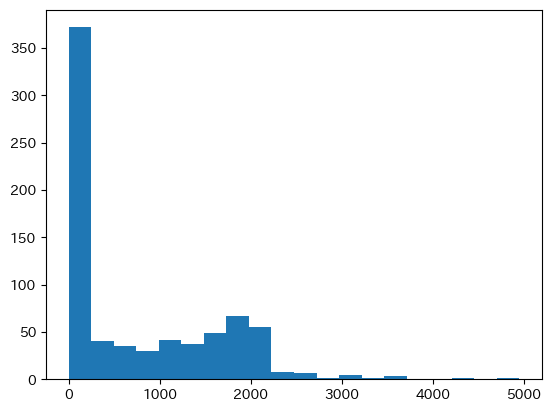
0に多くの観測値があることがわかる。
まず,下限の値を設定する。
left = 0
次に下限を示すarrayを作成する。
cond = (mroz['hours'] == left) # フィルターの作成
censor = np.zeros((len(mroz))) # 0のarrayの作成
censor[cond] = -1 # 条件に合わせて-1を代入
pd.Series(censor).value_counts() # Serieに変換し,内訳の確認
0.0 428
-1.0 325
Name: count, dtype: int64
次のコードでも同じ結果を得ることができる。
censor = mroz['hours'].apply(lambda x: -1 if x==left else 0)
まず先にcensorとmrozの行数が同じか確認しよう。
len(censor) == len(mroz)
True
確認できたので,推定してみよう。
formula = 'hours ~ 1 + nwifeinc + educ + exper + expersq + age + kidslt6 + kidsge6'
res_tobit = Tobit.from_formula(formula,
cens=censor,
left=0,
data=mroz).fit()
print(res_tobit.summary())
Optimization terminated successfully.
Current function value: 5.071839
Iterations: 2517
Function evaluations: 3635
Tobit Regression Results
===================================================================================
Dep. Variable: hours Pseudo R-squ: 0.034
Method: Maximum Likelihood Log-Likelihood: -3819.1
No. Observations: 753 LL-Null: -3954.9
No. Uncensored Obs: 428 LL-Ratio: 271.6
No. Left-censored Obs: 325 LLR p-value: 0.000
No. Right-censored Obs: 0 AIC: 7654.2
Df Residuals: 745 BIC: 7691.2
Df Model: 7 Covariance Type: nonrobust
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
Intercept 965.3052 446.430 2.162 0.031 90.318 1840.292
nwifeinc -8.8142 4.459 -1.977 0.048 -17.554 -0.075
educ 80.6456 21.583 3.737 0.000 38.343 122.948
exper 131.5643 17.279 7.614 0.000 97.697 165.431
expersq -1.8642 0.538 -3.467 0.001 -2.918 -0.810
age -54.4050 7.418 -7.334 0.000 -68.945 -39.865
kidslt6 -894.0218 111.878 -7.991 0.000 -1113.298 -674.745
kidsge6 -16.2180 38.640 -0.420 0.675 -91.950 59.515
Log(Sigma) 7.0229 0.037 189.514 0.000 6.950 7.096
==============================================================================
係数の解釈はOLSと同じようにおこなう。例えば,educの推定値は約80なので,教育年数が一年増えると平均で労働時間が年間80時間増加することを示している。またLog(Sigma)は切断回帰モデルの場合の解釈と同じである。
dir()やpy4macro.see()を使うことにより属性とメソッドを確認できる。
py4macro.see(res_tobit)
.aic .bic .bootstrap() .bse
.bsejac .bsejhj .conf_int() .cov_kwds
.cov_params() .cov_type .covjac .covjhj
.df_model .df_modelwc .df_resid .endog
.exog .f_test() .fitted_endog .fittedvalues
.get_nlfun() .hessv .initialize() .k_constant
.llf .llnull .llr .llr_pvalue
.load() .mle_retvals .mle_settings .model
.nobs .normalized_cov_params .obs .params
.predict() .prsquared .pvalues .remove_data()
.resid .result_null .save() .scale
.score_obsv .set_null_options() .summary() .t_test()
.t_test_pairwise() .tvalues .use_t .wald_test()
.wald_test_all_slopes .wald_test_terms()
この中にあるメソッドを使い,次の節では検定をおこなう。
検定と属性#
Wald検定を考えよう
Wald検定の例
\(H_0\):exper \(=\) expersq \(=0\) & kidslt6\(=\)kidsge6
\(H_A\):\(H_0\)は成立しない
検定方法は切断回帰のTruncregモジュールと同じである。
print( res_tobit.wald_test('exper=expersq=0, kidslt6=kidsge6', scalar=True).summary()
)
<Wald test (chi2): statistic=199.24993374297753, p-value=6.126737209322573e-43, df_denom=3>
\(p\)値は非常に低いため,1%有意水準でも帰無仮説を棄却できる。
次の3つの属性も有用である。
.fittedvalues:以下の式で与えられる線形の予測値 \(\hat{y}^{*}\)\[\hat{y}_i^{*}=\hat{\beta}_0+\hat{\beta}_1x_i\].fitted_endog:被説明変数の予測値 \(\text{E}(y|x)\) (正規分布に基づいた非線形).resid:以下の式で与えられる線形の残差\[\hat{u}_i=y_i-\hat{y}_i^{*}\]
y_star_hat = res_tobit.fittedvalues
u_hat = res_tobit.resid
plt.scatter(y_star_hat,u_hat)
pass
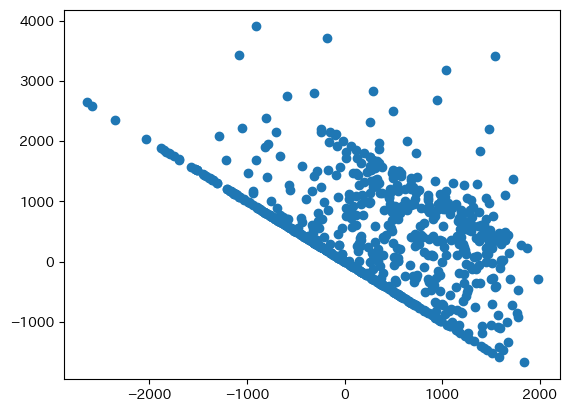
図の左下は切り打ちデータを反映している。
残差について#
切断回帰推定と同じように最尤法を使っているので,推定量の標準偏差の変化を使い残差の不均一について考えてみる。
# 通常の標準偏差
to0 = res_tobit.bse
# 不均一分散標準偏差
res_tobit_HC1 = Tobit.from_formula(formula,cens=censor,left=left,
data=mroz).fit(cov_type='HC1',disp=False)
to1 = res_tobit_HC1.bse
# 不均一分算標準偏差を使った場合の標準偏差の変化(%)
(100*(to1-to0)/to0)[:-1] # Log(Sigma)を省く
array([ 0.37098188, 1.45541926, 1.12857002, 7.83237821, 6.92967131,
-3.52864263, 4.88505645, 1.92222445])
全ての係数の標準誤差は大きくは変化しいない。それほど心配する必要もないかも知れない。
(注意)不均一分散の下でお最尤推定
推定量は一致性を満たさない
標準誤差も一致性を満たさない
不均一分散頑健標準誤差を使うことが推奨されることがあるが(研究論文でもそうする研究者も多い),もともと係数の推定量が一致性を満たさないため,
cov_typeで指定する不均一分散頑健標準誤差の有用性に疑問が残る。(参照)
Heckitモデル#
説明#
Heckitモデルは切断回帰モデルの拡張版であり,選択バイアス問題が疑われる場合に威力を発揮する。例を使って選択バイアス問題を考えてみよう。
<選択バイアス問題:例1>
大学4年生の学力を測るために,単位取得できる同じ試験を日本全国の大学4年生に受けさせるとしよう。この場合,勉強時間が短い学生は受験しない傾向にあるとしよう。
2つのシナリオ
シナリオ1:学生を無作為に選び(強制的に)受験させる。
シナリオ2:希望する学生だけに受けさせる。
結果
シナリオ1:ランダム抽出なので平均点は全体像を反映している。
シナリオ2:勉強時間が短い学生は受験しなくなり,平均点が上がることになる。全体像を歪める結果となる。
<選択バイアス問題:例2>
賃金に対する大学教育1年間の平均的効果を検証するとしよう。サンプルは大学卒業生と大学に進学しなかった高校卒業生。目的は全体像の把握であり,以下を考える。
\(W_{\text{大}}\):大卒の平均賃金
\(W_{\text{高}}\):高卒の平均賃金
次の仮定を置く:
教育が高いほど賃金は高い。
他の条件が同じであれば,教育が高いほど働く傾向にある(機会費用が高いため)。
2つのシナリオ
起こりえないシナリオ:卒業生を無作為に選び(強制的に)働かせて賃金のデータを集める。
現実的なシナリオ:自由に労働者が働くか働かないかを決め,働いている労働者のデータを集める。
結果:
起こりえないシナリオ:ランダム抽出なので(式1)は全体像を反映している。
現実的なシナリオ:教育水準が低い人(高卒)ほど働かな人いが多い傾向にある。特に,賃金が低い人ほど労働市場から退出する場合(労働供給の減少),高卒の平均賃金\(W_{\text{高}}\)は上昇することになり,(式1)は下落する。大学教育1年の効果は,低く推定され全体像を歪める結果となる。
これらの例が示唆するように,選択問題を無視して単純にOLS推定しても推定量にバイアスが発生する可能性がある。この問題に対処する推定方法の1つがHeckitモデルである。Heckitモデルは2段階で推定する。
<第1段階>
Probitモデルを使った2項選択に関する推定(例えば,労働市場に参加するしないの選択)
\(z_i^{*}\):選択に関する潜在変数(例えば,効用)
\(z_i\):選択を示す指標(例えば,1=働く,0=働かない)
\(w_i\):選択に影響する要因(例えば,働く時間に影響を及ぼす要因として幼児の数)
<第2段階>
第一段階の結果を使いOLS推定(例えば,賃金の推定)
\(y_i^{*}\):興味がある変数(例えば,労働者の賃金)
\(y_i\):実際に観測される\(y_i^{*}\)の値
\(x_i\):\(y_i^{*}\)に影響する要因(例えば,教育,経験)
ここで
\(\hat{k}_i\):第一段階における\(\dfrac{A-\hat{\alpha}_0-\hat{\alpha}_1w_i}{\sigma_u}\)の推定量
\(A=0\):下限の値
\(\sigma_e\):\(e_i\)の標準偏差
\(\sigma_u\):\(u_i\)の標準偏差
\(\rho=\text{Cov}(u_i,e_i)\)
(コメント)
ある仮定のもとで
Heckit推定量は一致性を満たす。Heckitを使わずに,(式6)を直接OLS推定すると\(\lambda\left(\hat{w}_i\right)\)を無視することになり,欠落変数バイアスが発生する。\(\rho=0\)の場合,(式6)を直接OLS推定しても欠落変数バイアスは発生しない。この場合,
Heckitモデルを使う必要はない。即ち,\(\rho\sigma_e\)のOLS推定量でバイアスが発生しいるか確認できる。
(注意)
上の説明では,\(w_i\)も\(x_i\)も1変数として説明したが,実際には複数の変数を使うことになる。その際,第1段階の説明変数(上の例では,\(w_i\))には第2段階の説明変数にない変数を1つ以上入れる必要がある。
Heckitモジュールの使い方#
statsmodelsもlinearmodelsもHeckit推定の正式モジュールがない。その代わりstatsmodelsに正式にmergeされていないHeckmanモジュールに基づいて著者が作成したheckitモジュールを使う。これにより上述の説明したステップに沿って自動で推定可能となる。
<使い方:ステップ1〜6>
今までstatsmodelsを使う場合,from_formulaメソッドを使ったが,それを使わない方法もある。Heckitの使い方はその方法に沿っている。
変数を準備する前準備
(式5)と(式6)を使った説明で,第1段階の被説明変数\(z_i\)と第2段階の被説明変数\(y_i\)は次のように連動していることに留意しよう。 $$
\[\begin{align*} &z_i=1\;\Rightarrow\; y_i=y^*_i\\ &z_i=0\;\Rightarrow\; y_i\text{は切断} \end{align*}\]$$
この点を利用し,
Heckitモジュールでは第1段階の被説明変数\(z_i\)を指定する必要がない。その代わりに,\(z_i=0\)の場合には\(y_i=\)NaNとなるように設定する必要がある。
第1段階と第2段階で使う全ての変数が入った
DataFrameを作成する。以下の説明ではdfと呼ぶ。第2段階の被説明変数を
endogとして定義する。例えば,dfの列yにある場合,以下のようにする。endog = df.loc[:,'y']
第2段階の説明変数だけを抜き取って
exogというDataFrameを作成し,それに定数項の列を加える。例えば,x1,x2,x3が該当する変数だとすると,以下のようにする。またexogに定数項を加える。exog = df.loc[:,[x1,x2,x3]] exog['Intercept'] = 1.0
第1段階の説明変数だけを抜き取って
exog_selectというDataFrameを作成し,それに定数項の列を加える。例えば,w1,w2,w3が該当する変数だとすると,以下のようにする。またexog_selectに定数項を加える。exog_select = df.loc[:,[w1,w2,w3]] exog_select['Intercept'] = 1.0
以下のように
Heckitを使い推定する。Heckit(endog, exog, exog_select).fit()
Warning
endog、exog、exog_selectの行数が全て同じになる必要がある。異なる場合はエラーが発生する。必ずlen()関数を使って確認しよう!
推定#
mrozを使った推定#
上で使ったmrozのデータセットを使い推定する。
第1段階の説明変数:
educ,exper,expersq,nwifeinc,age,kidslt6,kidsge6第2段階の被説明変数:
lwage第2段階の説明変数:
educ,exper,expersq
(目的)
教育の収益率の推定。
ステップ1
mrozにある変数inlfは,1975年に既婚女性が労働市場に参加した場合は1,参加しなかった場合は0になるダミー変数である。この変数を使い,変数作成の前準備として次の2点を確認する。
inlf=1の場合,lwageはNaNではない。inlf=0の場合,lwageはNaNである。
mroz.query('inlf == 1')['lwage'].isna().sum()
0
このコードの.isna()はlwageがNaNであればTrueを返す(isnan()ではないことに注意,またisnull()でも可)。その合計.sum()が0なので,「inlf=1の場合,lwageはNaNではない」ことが確認できた。
( ~mroz.query('inlf == 0')['lwage'].isnull() ).sum()
0
このコードの()の中を考えよう。上のコードと同じように,mroz.query('inlf == 0')['lwage'].isnull()はlwageがNaNであればTrueを返すが,その先頭に~をつけるとその逆のFalseを返すことになる。~は「反転」という意味である。その合計.sum()が0なので,「inlf=0の場合,lwageはNaNである」ことが確認できた。
ステップ2
mrosをそのまま使う。
ステップ3
第2段階の被説明変数を作成する。
endog = mroz.loc[:,'lwage']
ステップ4
第2段階の説明変数を作成する。
exog = mroz.loc[:,['educ', 'exper', 'expersq']]
exog['Intercept'] = 1.0
ステップ5
第1段階の説明変数を作成する。
exog_select = mroz.loc[:,['educ', 'exper', 'expersq','nwifeinc', 'age', 'kidslt6', 'kidsge6', ]]
exog_select['Intercept'] = 1.0
次のステップに進む前に、endog、exog、exog_selectの行数が同じか確認しよう。
len(endog) == len(exog) == len(exog_select)
True
ステップ6
推定を行う際,fit()にオプションを追加し不均一分散頑健標準誤差を指定する。
cov_type_1:第1段階推定でのオプションcov_type_2:第2段階推定でのオプション
(注意)
オプションを追加しない場合は,
nonrobustがデフォルトとなる。
res_heckit = Heckit(endog, exog, exog_select).fit(cov_type_2='HC1')
print(res_heckit.summary())
Heckit Regression Results
================================================================================
Dep. Variable: lwage R-squared: 0.156
Model: Heckit Adj. R-squared: 0.150
Method: Heckman Two-Step F-statistics: 26.148
Date: Sat, 20 Sep 2025 Prob (F-statistic): 0.000
Time: 00:35:20 Cov in 1st Stage: nonrobust
No. Total Obs.: 753 Cov in 2nd Stage: HC1
No. Censored Obs.: 325
No. Uncensored Obs.: 428
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
educ 0.1091 0.016 7.026 0.000 0.079 0.139
exper 0.0439 0.016 2.699 0.007 0.012 0.076
expersq -0.0009 0.000 -1.957 0.050 -0.002 1.15e-06
Intercept -0.5781 0.305 -1.895 0.058 -1.176 0.020
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
educ 0.1309 0.025 5.183 0.000 0.081 0.180
exper 0.1233 0.019 6.590 0.000 0.087 0.160
expersq -0.0019 0.001 -3.145 0.002 -0.003 -0.001
nwifeinc -0.0120 0.005 -2.484 0.013 -0.022 -0.003
age -0.0529 0.008 -6.235 0.000 -0.069 -0.036
kidslt6 -0.8683 0.119 -7.326 0.000 -1.101 -0.636
kidsge6 0.0360 0.043 0.828 0.408 -0.049 0.121
Intercept 0.2701 0.509 0.531 0.595 -0.727 1.267
================================================================================
coef std err z P>|z| [0.025 0.975]
--------------------------------------------------------------------------------
IMR (Lambda) 0.0323 0.134 0.241 0.809 -0.230 0.294
=====================================
rho: 0.049
sigma: 0.664
=====================================
First table are the estimates for the regression (response) equation.
Second table are the estimates for the selection equation.
Third table is the estimate for the coef of the inverse Mills ratio (Heckman's Lambda).
上段の表:第2段階推定
中断の表:第1段階推定
下段の表
IMR:逆ミルズ比((式6)の\(\lambda\left(\hat{w}_i\right)\))rho:第1・第2段階の誤差項の共分散((式6)の\(\rho\))sigma:第2段階誤差項の標準偏差((式6)の\(\sigma_e\))
(注意)表には通常の標準誤差が表示されている。不均一分散頑健標準誤差は以下で手動で計算する。
第2段階結果の属性とメソッドはdir()やpy4macro.see()で確認できる。
py4macro.see(res_heckit)
.HC1_se .bse .centered_tss .conf_int()
.corr_eqnerrors .cov_HC1 .cov_params() .cov_type_1
.cov_type_2 .df_model .df_resid .endog
.ess .exog .f_pvalue .f_test()
.fittedvalues .fvalue .initialize() .k_constant
.llf .load() .method .model
.mse_model .mse_resid .mse_total .nobs
.normalized_cov_params .params .params_inverse_mills .pinv_wexog
.predict() .pvalues .remove_data() .resid
.rsquared .rsquared_adj .save() .scale
.select_res .ssr .stderr_inverse_mills .summary()
.t_test() .t_test_pairwise() .tvalues .uncentered_tss
.use_t .var_reg_error .wald_test() .wald_test_terms()
.wendog .wexog .wresid
例えば,predict()は予測値を返す。ただ,この中にはまだ実装されていないものも含まれている。
また,この中にselect_resとあるが,この属性を使い第1段階推定のに関する属性・メソッドを確認できる。
py4macro.see(res_heckit.select_res)
.aic .bic .bse .conf_int()
.converged .cov_kwds .cov_params() .cov_type
.df_model .df_resid .f_test() .fittedvalues
.get_distribution() .get_influence() .get_margeff() .get_prediction()
.im_ratio .info_criteria() .initialize() .k_constant
.llf .llnull .llr .llr_pvalue
.load() .method .mle_retvals .mle_settings
.model .nobs .normalized_cov_params .params
.pred_table() .predict() .prsquared .pvalues
.remove_data() .resid_dev .resid_generalized .resid_pearson
.resid_response .save() .scale .score_test()
.set_null_options() .summary() .summary2() .t_test()
.t_test_pairwise() .tvalues .use_t .wald_test()
.wald_test_terms()
例えば,fittedvaluesは予測値を返す。次のコードでは基本統計量を表示できる。
print(res_heckit.select_res.summary().tables[0])
Probit Regression Results
==============================================================================
Dep. Variable: y No. Observations: 753
Model: Probit Df Residuals: 745
Method: MLE Df Model: 7
Date: Sat, 20 Sep 2025 Pseudo R-squ.: 0.2206
Time: 00:35:20 Log-Likelihood: -401.30
converged: True LL-Null: -514.87
Covariance Type: nonrobust LLR p-value: 2.009e-45
==============================================================================
この表にあるDep. Variable: yのyは第1段階の被説明変数を表しているが,第2段階の被説明変数lwageを使っているためこのような表記になっている。
結果の解釈#
第2段階推定の
educの係数は0.1091であり統計的に有意。
この結果を単純なOLSと比べよう。(lwageにあるNaNは自動的に除外される。)
formula = 'lwage ~ educ + exper + expersq'
res = smf.ols(formula, data=mroz).fit(cov_type='HC1')
print(res.summary().tables[1])
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
Intercept -0.5220 0.202 -2.589 0.010 -0.917 -0.127
educ 0.1075 0.013 8.131 0.000 0.082 0.133
exper 0.0416 0.015 2.722 0.006 0.012 0.072
expersq -0.0008 0.000 -1.931 0.053 -0.002 1.21e-05
==============================================================================
educのOLS推定値は0.1075でHeckit推定値と大きく変わらない。これは選択バイアスが殆どないことを示唆している。実際,IMR(逆ミルズ比)のp値は0.809であり,係数は0とする通常の有意水準で帰無仮説を棄却できない。即ち,単純なOLS推定では逆ミルズ比の欠落変数バイアスが発生していないことを意味する。
次に切断回帰推定を考えてみよう。
plt.hist(mroz['wage'].dropna(),bins=20)
pass
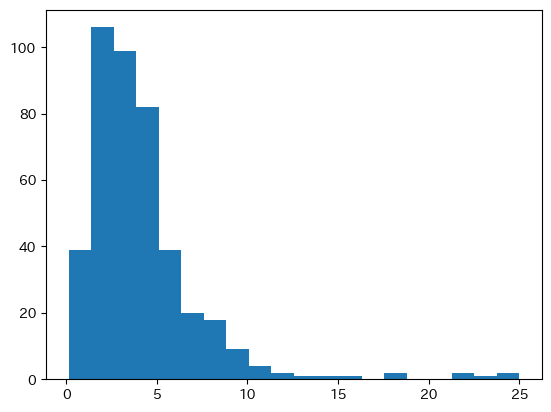
thresh = np.log(mroz['wage'].min()*0.5) # 左切断の下限
formula = 'lwage ~ 1 + educ + exper + expersq'
res_trunc = Truncreg.from_formula(formula, left=thresh,
data=mroz.dropna(subset=['lwage'])).fit()
print(res.summary().tables[1])
Optimization terminated successfully.
Current function value: 1.008409
Iterations: 68
Function evaluations: 122
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
Intercept -0.5220 0.202 -2.589 0.010 -0.917 -0.127
educ 0.1075 0.013 8.131 0.000 0.082 0.133
exper 0.0416 0.015 2.722 0.006 0.012 0.072
expersq -0.0008 0.000 -1.931 0.053 -0.002 1.21e-05
==============================================================================
この推定では,wageの最小値の50%の値の対数を下限の値に設定している。wage=0を下限にしてもよいが,その場合,np.log(0)はマイナス無限になり,通常の最尤推定と同じになる。切断回帰推定を使っても結果は変わらない。即ち,選択バイアスが大きな問題ではないことを示唆している。
第1段階推定ではProbitモデルを使っているが,以下では不均一分散に関して検定を行う。
het_test_probit(res_heckit.select_res)
H0: homoscedasticity
HA: heteroscedasticity
Wald test: 8.665
p-value: 0.278
df freedom: 7
帰無仮説は棄却できない。推定量の一致性は満たされていると考えて良いだろう。

