SciPy.stats#
import japanize_matplotlib
import matplotlib.pyplot as plt
import numpy as np
# 警告メッセージを非表示
import warnings
warnings.filterwarnings("ignore")
SciPy(サイパイ)は,NumPyの大幅な拡張版と理解して良い。SciPyを読み込むとNumPyの関数などを利用できるようになる。しかしSciPyは大きなパッケージであり,全てを読み込む必要もない。従って,NumPyを読み込んで,SciPyのサブパッケージや関数を読み込むということで十分であろう。ここではSciPyのstatsというサブパッケージについて説明する。
正規分布(Normal Distribution)#
正規分布のモジュール名はnormであり,以下が主な関数である。
確率密度関数:
norm.pdf(x, loc=0, scale=1)pdfはProbability Density Functionの頭文字loc= 平均scale= 標準偏差x= \(-\infty\)から\(\infty\)の間の値返り値:
xの値が発生する確率(%)locとscaleを省略すると標準正規分布の確率密度関数となる。
累積分布関数:
norm.cdf(x, loc=0, scale=1)cdfはCumulative Distribution Functionの頭文字loc= 平均scale= 標準偏差x= \(-\infty\)から\(\infty\)の間の値返り値:
x以下の値が発生する確率(%)locとscaleを省略すると標準正規分布の累積分布関数となる。
パーセント・ポイント関数:
norm.ppf(a, loc=0, scale=1)ppfはPercent Point Functionの頭文字loc= 平均scale= 標準偏差a= 0 ~ 1の間の値返り値:累積分布関数の値が
aである場合のxの値(累積分布関数の逆関数)locとscaleを省略すると標準正規分布のパーセント・ポイント関数となる。
ランダム変数生成関数:
norm.rvs(loc=0, scale=1, size=1)rvsはRandom VariableSの大文字の部分loc= 平均scale= 標準偏差size= 生成されるランダム変数の数返り値:正規分布に従って発生したランダム変数
locとscaleを省略すると標準正規分布のランダム変数生成関数となる。
scipy.statsのnormを読み込む。
from scipy.stats import norm
確率密度関数
norm.pdf(0)
0.3989422804014327
0が発生する確率は約39.9%とわかる。norm.pdf(x)のグラフを描くためには,\(\infty\)から\(\infty\)のxの返り値が必要になるが,ここでは-4から4の区間で100個のxの値で近似する。
x = np.linspace(-4, 4, 100)
このxを直接norm.pdf()に代入すると,全てのxの値に対しての返り値を得ることができる。それをy_pdfに割り当てる。
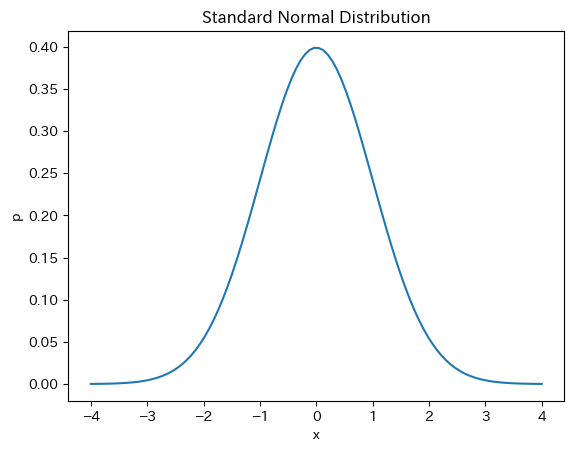
y_pdf = norm.pdf(x) # 標準正規分布
plt.plot(x,y_pdf)
plt.xlabel('x')
plt.ylabel('p')
plt.title('Standard Normal Distribution')
pass
累積分布関数
y_cdf = norm.cdf(x) # 標準正規分布
plt.plot(x, y_cdf)
plt.xlabel('x')
plt.ylabel('P')
plt.title('Cumulative Distribution Function')
pass
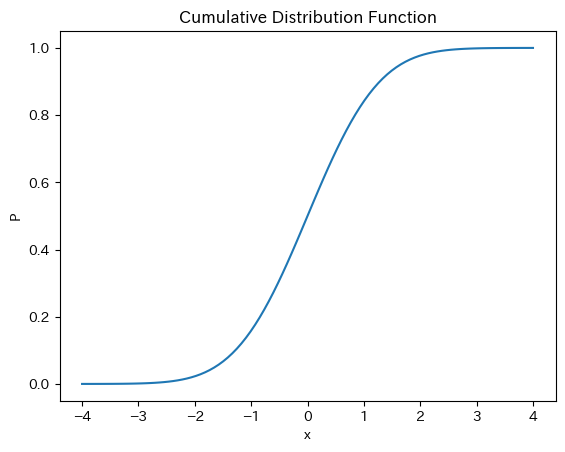
この関数を使うことにより,xの値が\(X\)の時,それ以下の値が発生する確率は何%かを計算できる。例えば,xが\(0\)以下の値を取る確率は
norm.cdf(0)
0.5
確率密度関数が平均\(0\)(loc=0)を中心に左右対称のため確率は50%となる。では,xが\(-4\)以下の場合は?
norm.cdf(-4)
3.167124183311986e-05
返り値の最後のe-05は\(\times 10^-5\)という意味。では,xが4以上の確率は?
1-norm.cdf(4)
3.167124183311998e-05
パーセント・ポイント関数
p = np.linspace(0,1,100)
y_ppf = norm.ppf(p) # 標準正規分布
plt.plot(p,y_ppf)
plt.xlabel('P')
plt.ylabel('x')
plt.title('Percent Point Function')
pass
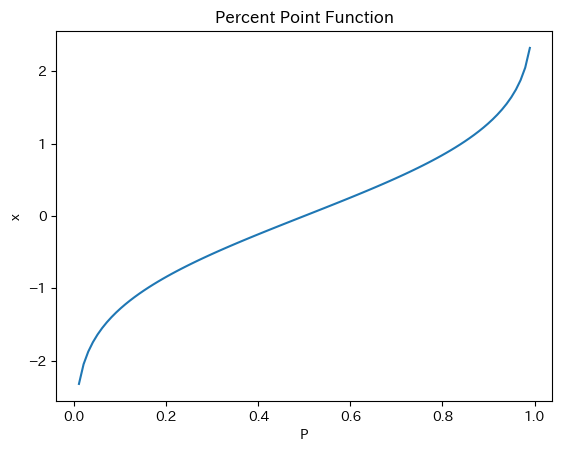
パーセント・ポイント関数を使い,累積分布関数の値がPである場合のxの値を計算できる。P=0.5の場合のxは?
norm.ppf(0.5)
0.0
P=0.025の場合のxは?
norm.ppf(0.025)
-1.9599639845400545
P=0.975の場合のxは?
norm.ppf(0.975)
1.959963984540054
ランダム変数生成関数
10000個のランダム変数を生成しよう。
y_rvs = norm.rvs(size=10_000) # 標準正規分布
plt.hist(y_rvs, bins=30) # bins=表示する棒の数(デフォルトは10)
pass
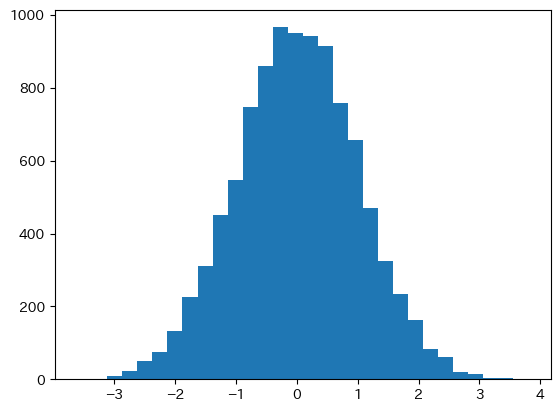
y_rvsは標準正規分布から生成されたが,y_rvsがどの分布関数から生成されたか不明だったとしよう。更に,y_rvsから元の確率密度関数を推定したいとしよう。その際に使う手法をカーネル密度推定と呼ぶ。SciPyにはそのための関数gaussian_kdeが用意されている。gaussian(ガウシアン)とは天才数学者ガウスの名前からきており「ガウス的な」と理解すれば良い。kdeはKernel Density Estimate(カーネル密度推定)の頭文字をとっている。
from scipy.stats import gaussian_kde # サブパッケージを読み込む
kde = gaussian_kde(y_rvs) # y_rvsから確率密度関数を推定
plt.plot(x, kde(x)) # 横軸のxに対してプロット
pass
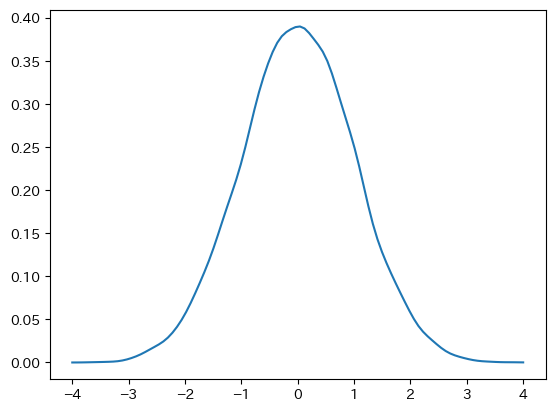
推定なので標準正規分布の確率密度関数と全く同じにはならないが,非常に近い。上の図と重ねると。
plt.hist(y_rvs, bins=30, density=True)
plt.plot(x, kde(x))
pass
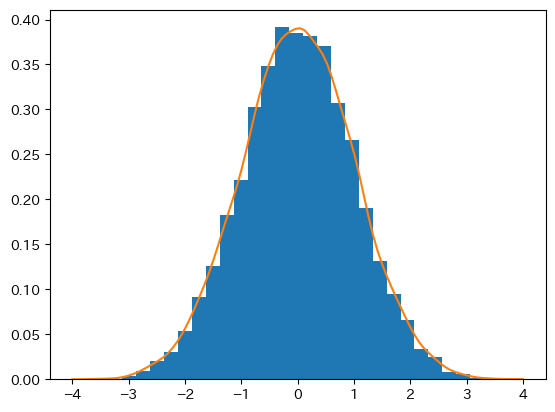
plt.hist()にあるdensity=Trueは縦軸を%表示にする引数である。これによりplt.histのヒストグラムとplt.plot()のカーネル密度関数が同じスケールで表示されることになる。
その他の分布関数#
\(t\)分布#
\(t\)分布のモジュール名はt。
t.pdf(x, df)
t.cdf(x, df)
t.ppf(a, df)
t.rvs(df, size=1)
df:自由度(degree of freedom)
scipy.statsのtを読み込み確率密度関数の図を表示する。
from scipy.stats import t
x = np.linspace(-4,4,100)
y = t.pdf(x, df=1)
plt.plot(x,y)
pass
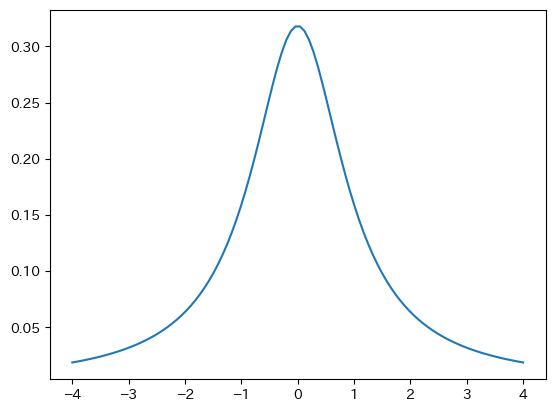
df=1の場合にxの値が-3以下の確率は何か?
t.cdf(-3, df=1)
0.10241638234956672
df=1の場合にxの値が3以上の確率は何か?
1-t.cdf(3, df=1)
0.10241638234956674
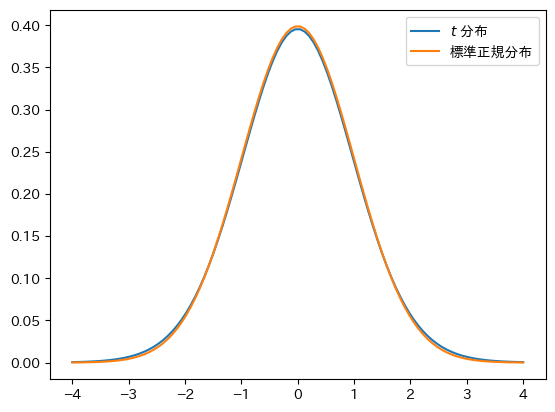
\(t\)分布と標準正規分布は正規分布は非常に類似性が高い。自由度が30になれば,両分布の誤差は非常に小さくなることが知られている。確認するために,プロットしてみよう。
x = np.linspace(-4, 4, 100)
plt.plot(x, t.pdf(x, 30), label=r'$t$ 分布')
plt.plot(x, norm.pdf(x), label='標準正規分布')
plt.legend()
pass
\(\chi^2\)分布#
\(\chi^2\)分布のモジュール名はchi2。
chi2.pdf(x, df)
chi2.cdf(x, df)
chi2.ppf(a, df)
chi2.rvs(df, size=1)
df:自由度(degree of freedom)
scipy.statsのchi2を読み込み確率密度関数の図を表示する。
from scipy.stats import chi2
x = np.linspace(0,12,100)
y = chi2.pdf(x, df=3)
plt.plot(x,y)
pass
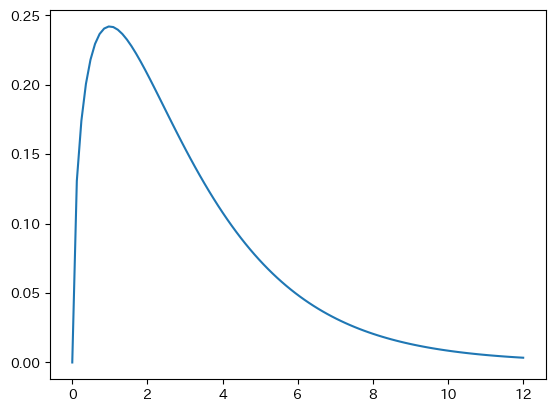
df=3の場合にxの値が1以下の確率は何か?
chi2.cdf(1, df=3)
0.19874804309879915
df=3の場合にxの値が10以上の確率は何か?
1-chi2.cdf(10, df=3)
0.0185661354630432
\(F\)分布#
\(F\)分布のモジュール名はf。
f.pdf(x, dfn, dfd)
f.cdf(x, dfn, dfd)
f.ppf(a, dfn, dfd)
f.rvs(dfn, dfd, size=1)
dfn:分子の自由度(numerator degree of freedom)dfd:分母自由度(denominator degree of freedom)
scipy.statsのfを読み込み確率密度関数の図を表示する。
from scipy.stats import f
x = np.linspace(0.001,5,1000)
y = f.pdf(x, dfn=5, dfd=1)
plt.plot(x,y)
pass
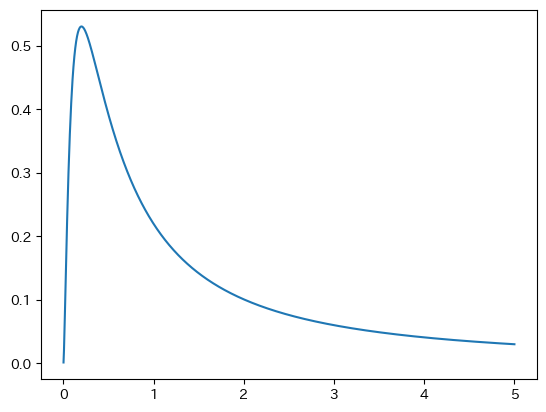
dfn=5, dfd=1の場合にxの値が0.1以下の確率は何か?
f.cdf(0.1, dfn=5, dfd=1)
0.02503101581845294
dfn=5, dfd=1の場合にxの値が5以上の確率は何か?
1-f.cdf(5, dfn=5, dfd=1)
0.32657156446244606
一様分布 (Uniform Distribution)#
一様分布のモジュール名はuniform。
uniform.pdf(x, loc=0, scale=1)
uniform.cdf(x, loc=0, scale=1)
uniform.ppf(a, loc=0, scale=1)
uniform.rvs(loc=0, scale=1, size=1)
loc:xの最小値scale:xの幅xの最大値:loc+scale
mだけ「右」に平行移動させる場合は
loc=m # scaleは省略
scipy.statsのuniformを読み込み確率密度関数の図を表示する。
from scipy.stats import uniform
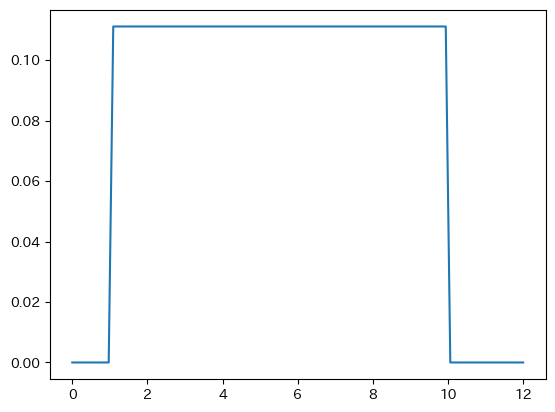
x = np.linspace(0,12,100)
y = uniform.pdf(x, loc=1, scale=9)
plt.plot(x,y)
pass
ロジスティク分布(Logistic Distribution)#
ロジスティック分布のモジュール名はlogistic。
logistic.pdf(x, loc=0, scale=1)
logistic.cdf(x, loc=0, scale=1)
logistic.ppf(a, loc=0, scale=1)
logistic.rvs(loc=0, scale=1, size=1)
loc:平均値scale:分散に影響する値
logistic.pdf(x,loc,scale) = logistic.pdf(z), z=(x-loc)/scale
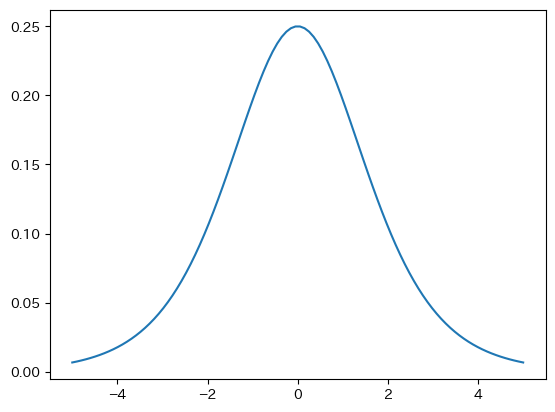
scipy.statsのlogisticを読み込み確率密度関数の図を表示する。
from scipy.stats import logistic
x = np.linspace(-5,5,100)
y = logistic.pdf(x)
plt.plot(x,y)
pass